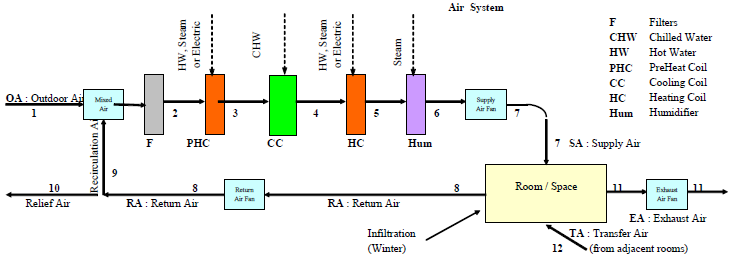
Piping and Ductwork Systems
Piping systems are used to distribute liquids. Ductwork systems are used to distribute gases. The mechanical system used to move the liquid is a pump and the mechanical system used to move the gas is a fan. Pumps and fans are driven by electric motors.
Fluids
The term "Fluid" consists of gases and liquids. Fluids have a definite mass and volume at a given temperature and pressure. They have no consistent shape when it is not confined a container. They cannot sustain shear (lateral) stress under equilibrium conditions. They cannot be torn, fractured or broken into smaller pieces.
Gases are fluids that do not have a definite volume. A gas has no shape and it assumes the volume of the container that it is confined in. Gases can be compressed. They are affected by temperature and pressure. The gas volume in an enclosed container is the container volume. Two containers of different volumes can contain the same mass of gas.
Liquids are fluids that have a definite volume of their own that is independent of the shape and volume of the container. When a liquid is placed in a container, it assumes the shape of the container but the volume and mass remain the same under constant temperature and pressure. Liquids can be considered non-compressible. The volume will not change significantly under pressure. The volume of the liquid can change appreciably at different temperatures.
Pressure (P):
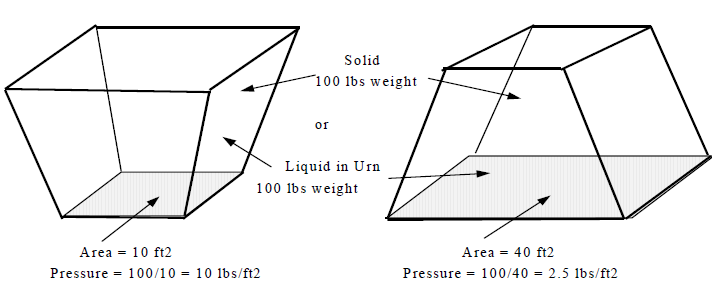
Pressure is the force per unit area. The pressure exerted by a force or weight of 100 lbs on 10 ft2 is (100 lbs / 10 ft2) 10 pound per square foot (1 psf). The same weight resting on 40 ft2 is (100 lbs / 40 ft2) is 2.5 pounds per square foot (2.5 psf) or 2.5 lbs on 144 square inches = 0.01736 pounds per square inch (psi).
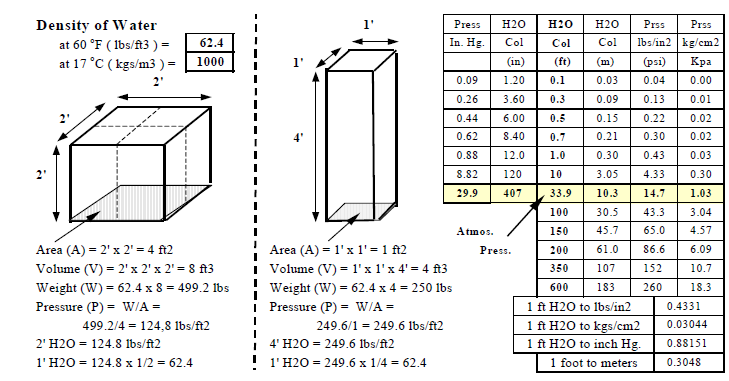
Density (d) is the mass per unit volume. Example: Density of water is approximately 62.4 pounds per cubic foot (I-P) and 1000 kilograms per cubic meter (S-I) at normal pressure and temperature.

Pressure Units as Height of Column of Water
Figure ? shows that a measuring scale for pressure can be the height of a column of liquid. For example the density of water is 62.4 lbs/ft3. The pressure at the bottom of a tank with any surface areas and containing water to a height of 1 foot is 62.4 lbs/ft2 and at a height of 4 feet it is 4 times the pressure that of 1 foot. The first tank in the figure contains 500 lbs of water but the pressure at the bottom of the tank of height 2 feet is 2 x 62.4 = 128.4 lbs/ft2. The second tank contains 250 lbs of water but the pressure at the bottom of the tank of height 4 feet is 4 x 62.4 = 249.6 lbs/ft2.
Pressure can therefore be expressed as the height of a column of water. In the case of liquids (water) and pumping systems it is measured in feet of water. However, the pressure of steam is measured in psi. In the case of gases (air) and fan systems it is meaured in inches of water.
Atmospheric Air Pressure
The term "air" when referred to in comfort air-conditioning consists of water vapor and dry air (DA) which consists of the rest of gases in the mixture of gases. Steam (water, H2O) is not a mixture of different substances but a stand-alone chemical compound.
The surface of the earth is covered with air. Like all object masses, the mass of air is attracted towards the planet earth by gravity. Traces of air can exist up to 200 miles ( 1 million feet) above the earth. However, 90 percent of the mass of atmospheric air is within 10 miles (53,000 feet, 16,100 meters) of the earth's surface.
This mass of air exerts a pressure on the surface of the earth and this is called atmospheric air pressure. On average this pressure at sea level is approximately 14.7 pounds per square inch or psi ( 34 feet (10.3 meters) of water, 30 inches (750 millimeters ) of mercury, 1 kilogram per square centimeter. Pressure is also measured in atmospheres where 1 atmosphere = 14.7 psi.
The highest point of the earth above sea level is Mount Everest in the Himalayan mountain range separating India and Tibet in China. The height of land measured above sea level is called elevation above sea level or altitude and the altitude of Mt. Everest is 29,029 feet (8,948 meters). The highest capital city of a country is La Paz in Bolivia, South America which is at an altitude of 12,000 feet. Passenger aircraft fly at altitudes of 20,000 to 70,000 feet and this height is still well within the earth's gravitational pull.
The density (lbs/ft3) of air therefore decreases with the elevation above sea level of the location. Since we breathe in the same volume of air at any elevation, the mass amount (lbs) of air, and consequently the amount of oxygen, that we breathe in decreases with increasing elevations. The decrease in density also affects the operation of several types of equipment that use or handle air. These equipment are therefore rated for zero elevation and they have to be reconfigured or reselected for higher elevations.
The pressure of liquids is measured in feet of water and the pressure of gases is measured in inches of water. Steam is also a gas, but the pressure of steam is measured in pounds per square inch (psi). The pressure of atmospheric air is measured in inches of mercury (in.Hg.). The choice of measuring fluid has to do with convenience and practicality. For instance all situations (air, water, gases, liquids) could be based on one set of units such as psi. This would produce very large or very small values for the different situations.
The density of air also varies with the temperature as shown in the table below. Outdoor air at -20oF is much denser or heavier than the air at 70oF indoor temperature. Outdoor air in winter is therefore at a higher pressure than the air indoors. This results in the infiltration of outdoor air through the building envelope (cracks around the windows and doors and through porous walls) into the indoor space.

Figure -
| Temp | Density | Temp | Density | Temp | Density | Temp | Density |
| oF | lbs/ft3 | oF | lbs/ft3 | oF | lbs/ft3 | oF | lbs/ft3 |
| -60 | 0.099 | 20 | 0.083 | 70 | 0.075 | 130 | 0.065 |
| -20 | 0.090 | 32 | 0.081 | 90 | 0.072 | 150 | 0.065 |
| 0 | 0.086 | 50 | 0.078 | 110 | 0.070 | 212 | 0.059 |
Table -
Gauge Pressure
Every surface or object on the earth has the weight of the atmosphere resting on it. The absolute weight or pressure exerted by a substance is therefore the weight of the substance resting on the weighing scale plus the weight of air covering the weighing scale. The sum of these two pressures is called absolute pressure. The pressure exerted by the atmosphere can be ignored for everyday situations and we can measure pressures and weights above atmospheric pressure.
The pressure that excludes atmospheric pressure is called gauge pressure. The absolute pressure cannot be ignored in scientific calculations since the atmospheric pressure varies with altitude. The absolute units for pressure must be used in dealing with equations such as the Gas Laws.
Absolute Pressure (psia) = Gauge Pressure (psig) + 14.7 psi (atmospheric pressure)
Gauge Pressure (psig) = Absolute Pressure (psia) - 14.7 psi (atmospheric pressure)
It is impossible to make a pressure measurement on the earth's surface unless it is made relative to atmospheric pressure. Pressure gauges, piezometers and all pressure measuring devices indicate gauge pressure, that is pressure above 14.7 psia. Zero psia is supposed to be a perfect vacuum. This cannot be achieved in practice.

Measuring Pressure

The instrument used to measure atmospheric pressure is called a barometer. Mercury is used to measure this pressure since an instrument using a column of water that is 34 feet high is not practical. The density of mercury is 849.4 lbs/ft3 compared to 62.4 lbs/ft3 of water. The principle of measuring atmospheric pressure is shown in Figure - ?. A tube that is closed at one end is first inverted and filled with the liquid being used to measure pressure.
The open end is next held closed and turned over and then immersed in a tank containing the same liquid. The end is then opened. The liquid in the tube will rise until it reaches a height that has the same equivalent pressure of the atmosphere at the level of the tank. The space above the level in the tube is a vacuum at 0 pressure. As with measuring temperature, the mercury barometer is not suitable for measuring very high and low pressures and other types of instruments are used.
Duct and Pipe Sizing.
Ducts are made typically of thin lightweight galvanized steel or aluminum (10 to 22 gauge) and they are used to distribute air and gases. Duct shape can be round, rectangular or oval. Pipes are made of are made of steel, copper, cast iron and other heavier materials and they are used to distribute water and liquids. Pipes are always round.
Gases and liquids are both fluids and they differ in their properties of density, kinematic viscosity and specific heat. The pipe sizing principles, theory and equations for both ducts (gases) and pipes (liquids) are the same. Ducts are first sized as round and then the equivalent rectangular and oval sizes are determined to produce the same pressure drop as the round duct.
The following section shows the pipe/duct sizing and heat gain/loss equations. Pipe and duct design computer programs use these equations. However charts (graphs) generated by the equations are used for sizing pipes and ducts manually. In the case of rectangular ducts, tables are provided for converting round ducts to equivalent rectangular ducts.
Pipe (and Round Duct) Sizing
The general principles of pipe sizing are described in the ASHRAE Handbook: 1985 Fundamentals, Chapter 34, p. 34.1. The Darcy-Weisbach and Colebrook-White equations are used to calculate the pressure drop in a pipe section due to fluid friction. The Darcy-Weisbach equation is:
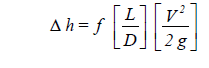
| where | Δ h | = head loss due to friction (ft) |
| f | = friction factor, dimensionless | |
| D | = inside diameter of pipe (ft) | |
| L | = length of pipe section (ft) | |
| V | = average velocity (ft/sec) | |
| g | = acceleration of gravity (ft/sec2) |
The friction factor f is a function of the pipe roughness Δ, inside diameter D and a dimensionless parameter, the Reynolds number.
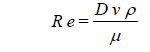
| where | ρ | = fluid density at given temperature (lb/cu ft) |
| μ | = dynamic viscosity of fluid (lb/ft sec) |
Laminar flow exists where Re < 2100. For this condition, the friction factor f is obtained from:
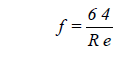
Where Re > 2100, the flow is assumed to be turbulent. The Moody diagram that relates the friction factor f with Reynolds number and the relative roughness /D is shown in ASHRAE Handbook: 1985 Fundamentals, p. 2.10, fig. 13. The Colebrook-White equation for turbulent flow, shown in Equation 20, is used for the friction factor f.
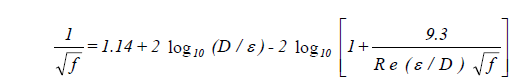
where ε = absolute roughness of inside pipe wall (ft)
For fully rough flow, the value of Reynolds number is high and the last term in Equation 20 can be neglected. Equation 21 can be used in its place.
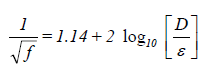
Equation 20 is used to calculate the friction factor f for turbulent flow. The Newton-Raphson iterative method is used to solve for f since f appears on both sides of the equation. The initial value of f for this iteration is obtained from Equation 21. As Reynolds number increases, the values from Equation 20 approach those that would be obtained by applying Equation 21 directly for fully rough flow.
Pipe sizing and the size of each pipe section depend on your criteria. The criteria can be based on the limits for pressure loss per 100 ft, maximum velocity or maximum flow. The sizing iteration consists of comparing the pressure drop/100 ft, velocity or flow against the limits you specify. This is done for each standard pipe size, beginning with the smallest size and continuing until a size is found that meets the criteria. When the maximum pipe size limit is reached, you must use your engineering judgment to decide whether to:
- maintain the sizing criteria and increase the pipe size above the maximum limit or
- maintain the pipe size limit and calculate the new criteria for this size.
| Liquid | Properties | Temperature oF | ||||||
| -30 | 0 | 30 | 60 | 100 | 150 | 212 | ||
| WATER | Density (lb/cu ft) Kinematic viscosity (sq ft/sec) Specific heat (Btu/lb oF) | 62.4220 .0 1.0 | 62.37 12.17 1.0 | 62.00 7.39 1.0 | 61.20 4.76 1.0 | 59.81 3.2 1.005 | ||
| GLYCOL | Density (lb/cu ft) Kinematic viscosity (sq ft/sec) Specific heat (Btu/lb oF) | 67.98 595.0 0.70 | 67.55 190.0 0.73 | 67.11 85.4 0.76 | 66.55 48.6 0.78 | 65.74 22.6 0.81 | 64.68 12.5 0.85 | 63.12 6.4 0.88 |
| AIR | Density (lb/cu ft) Kinematic viscosity (sq ft/sec) Specific heat (Btu/lb oF) | 0.075 ? 0.24 | ||||||
Fig.: Properties of Liquids (Water, Glycol and Brine)
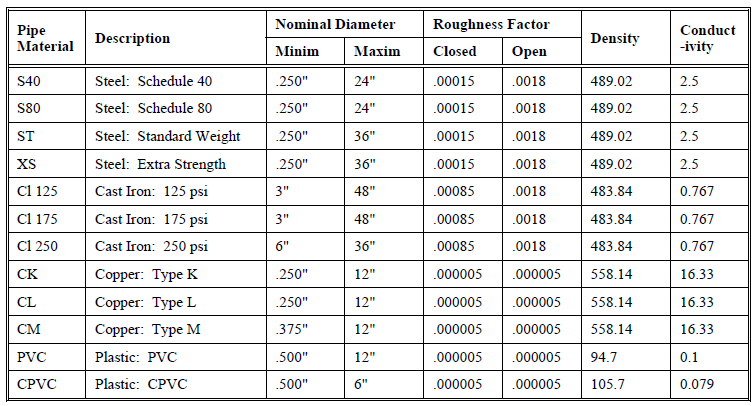
Fig: Properties of Pipe Materials used in Buildings
Thermal Analysis of Pipes
The heat gain/loss and temperature calculation options apply to liquids and steam only.
You can choose between two options for determining the fluid temperature in each pipe section. In the first option, you can assume an average supply and return fluid temperature for all supply and return sections. This data is used to calculate the fluid properties. An example of the use of average temperatures is 200oF supply and 160oF return for a hot water heating system.
In the case of uninsulated pipes and high temperature steam and hot water, the supply temperature at each terminal must be calculated. This is done by calculating the entering and leaving temperature of each supply section, beginning with the initial temperature of the first section. The first section must be identified. In the case of liquids, the first section is the section downstream of the pump station.
The entering temperature of any supply section is the leaving temperature of the upstream section. You can reset the leaving section temperature for sections that have primary equipment.
The following equations are used to calculate liquid and steam heat gains and losses:
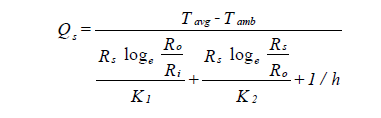
| where | Qs | = rate of heat transfer per square foot of outer surface (Btu/hr sq ft) |
| Tavg | = average temperature of section (oF) | |
| Tamb | = temperature of ambient air (oF) | |
| Ri | = inside radius of pipe, (in.) | |
| Ro | = outside radius of pipe, (in.) | |
| Rs | = outside radius of insulation (in.) - Ro + insulation thickness | |
| K1 | = thermal conductivity of pipe (Btu in./hr sq ft oF) | |
| K2 | = thermal conductivity of insulation (Btu in./hr sq ft oF) | |
| 1/h | = outside surface resistance (hr sq ft oF/Btu in. = 0.6) |
Equation 12 is based on heat flow Equations 11 and 12 in ASHRAE Handbook: 1981 Fundamentals, p. 23.8. The average temperature of the section is the mean value of the temperatures entering and leaving the section. Since the leaving temperature is unknown, the average temperature is calculated iteratively.
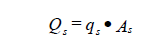
| where | Qs | = total rate of heat transfer from pipe section (Btu/hr) |
| As | = outside surface area of pipe (sq ft) |
The temperature of the liquid flowing through the pipe section is obtained from Equation 14. The procedure for determining steam temperature changes is described in Steam Piping.

| where | dTs | = change in liquid temperature in section (oF) |
| Fs | = flow through section (GPM) | |
| Df | = density of liquid (lb/cu ft) | |
| Cp | = specific heat of liquid (Btu/lb oF) |
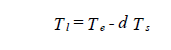
| where | T1 | = temperature of fluid leaving section (oF) |
| Te | = temperature of fluid entering section ( oF) |
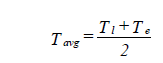
The average temperature Tavg in Equation 12 depends on the leaving section temperature in Equation 16. The procedure consists of initializing the leaving temperature to the entering section temperature and then iterating through Equations 12 through 16 until a steady state value of Tavg occurs
Frictional Losses for Noncircular Ducts
All friction loss calculations are based on the equivalent hydraulic diameter. With equal length of round and rectangular ducts, constant flow in each duct, and equal resistance to flow in both the round and rectangular ducts, the equivalent round of a rectangular duct is calculated by:
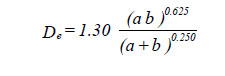
| where | De | = circular equivalent of a rectangular duct for equal length, fluid resistance and air flow (in.) |
| a | = length of one side of duct (in.) | |
| b | = length of adjacent side of duct (in.) |
The mean velocity in a rectangular and oval duct will be less than its circular equivalent.
For oval ducts, the corresponding equations are:
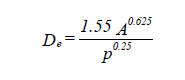
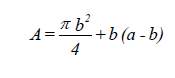

where
p = perimeter of oval duct (in.)
a = length of major axis (in.)
b = length of minor axis (in.)
For both rectangular and oval ducts, the length of the sides is initially determined by the target aspect ratio. If the resulting dimensions fall outside the minimum and maximum allowable limits you have set, the dimensions are recalculated without using the target aspect ratio.
Dynamic Losses
Dynamic losses are caused by restrictions and changes in direction to the flow through a piece of equipment (volume damper, heating coil, etc.) and duct fittings. HVAC Systems Duct Design, SMACNA, 1985 lists the fittings available for round and rectangular ducts. Since little dynamic loss data for oval fittings are available, the data for rectangular fittings are used as an approximation.
Fittings
A duct fitting can occur anywhere along the length of a duct section. The program does not limit the number of fitting types or multiples thereof per duct section. If a fitting type is not available in the tables, its dynamic loss has to be entered as a special loss.
All the necessary engineering performance information for fittings is provided in the Ducts Program. The engineering design effort is to locate the appropriate fitting type in the duct network system. The duct fitting type and shape type should be compatible. Fittings are classified as junctions, transitions, and elbows.
| Junctions | Junctions are fittings which split the air stream into two or more branches. Converging junctions join two or more air streams into one and are basically used in a return/extract duct system. Fittings called take-offs, tees, and wyes are in this category. Loss coefficients for junctions are functions of the duct dimensions, air velocities and airflow rates. |
| Transitions | Transitions are fittings which change the duct size or shape without changing airflow direction or airflow rate. Transitions can be con-verging or diverging. Loss coefficients for transitions are functions of upstream and downstream duct velocities, angle of transition, transition length, and Reynolds number, Re. |
| Elbows | Elbows are fittings which change the direction of the air stream without changing the air quantity or velocity. The loss coefficients of elbows are functions of the elbow radius, duct dimensions, angle of turn, and Reynolds number, Re. |
By definition, a new duct section occurs when there is a change in air quantity, velocity, shape, duct material or duct insulation. Every duct section, therefore, begins with a junction or transition type fitting. These fittings are commonly referred to as take-off fittings. There is always one, and only one, take-off fitting per duct section.
Fitting Losses
Methods of computing the energy losses from the various fitting types are based on information found in ASHRAE Handbook: 1981 Fundamentals p. 33.28 through 33.50
The fluid resistance coefficient represents the ratio of the total pressure loss to the dynamic pressure at the referenced cross-section O:
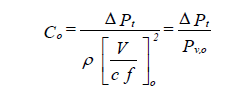
where
| cf | = conversion factor (1097) |
| ΔPt | = total losses of fitting in terms of total pressure (in. of water) |
| Co | = overall fluid resistance coefficient referenced to section O, dimensionless |
| V | = average velocity to which coefficient Co is referenced (ft/min) |
| Pv,o | = velocity pressure (in. of water) |
| ρ | = fluid density (lbm/cu ft) |
For entries, exists, elbows and transitions, the fitting total pressure loss at section is calculated by:
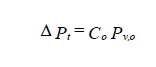
where the subscript o is the cross section at which the velocity pressure is referenced.
For converging and diverging flow junctions, the total pressure loss through the main section is calculated as:
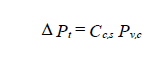
For total pressure losses through the branch section
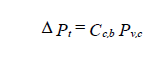
where
| Cc,s | = main local coefficient, dimensionless |
| Cc,b | = branch local coefficient, dimensionless |
| Pv,c | = velocity pressure at the common section, c |
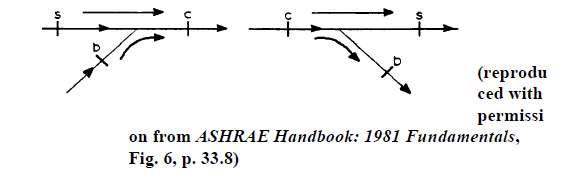
A tee nomenclature is shown in Fig. 1-7 for converging and diverging flow junction where,

| Duct Material | Roughness factor ft |
| Uncoated Carbon Steel, Clean | 0.00015 |
| Aluminum | 0.0002 |
| Galvanized Steel, Hot Dipped | 0.0005 |
| Stainless Steel | 0.0003 |
| Fibrous Glass Duct, Rigid | 0.0003 |
| Flexible Duct, Metallic | 0.007 |
| Fibrous Glass Duct Liner | 0.015 |
Fig: Duct Material Absolute Roughness
Sizing Methods
The sections of supply duct systems can be sized using one of the following methods:

Equal friction and constant velocity methods are used for manual duct sizing. Static regain and total pressure methods require the use of computer programs. Velocity reduction is a “rule of thumb” method. Constant velocity is used for short runs of ductwork such as flexible ducts. Flexible ducts are always considered round in shape.
Equal Friction Sizing Method
This is the most commonly used method for duct and pipe sizing. It can be done manually using charts generated for a particular gas or liquid fluid (using the properties of the fluid) and a particular duct or pipe material (using the properties of the pipe material).
In the equal friction method, the system is sized for a constant pressure loss per unit length of duct. The equal friction method can be used for the design of supply and extract duct systems. The equal friction sizing method works iteratively between the minimum and maximum velocity limits to determine a duct size that results in the specified pressure loss per unit length.
Static Regain Sizing Method
For this method, a section of the duct system is sized so that the increase in static pressure due to velocity reduction from its upstream section, offsets the friction loss in the section.
The advantage of this method is that all sections have approximately the same entering static pressure, thereby simplifying outlet selection. One disadvantage might be seen in networks with a large pressure drop in a section near the fan outlet. The velocity could be reduced to the minimum within a few sections in such a way that all the ductwork downstream would be sized using minimum velocity. Another disadvantage could stem from specifying a very low minimum velocity. Ducts would then tend to be very large at the end of long branch runs. The sizing method does not account for the total mechanical energy supplied to the air by the fan.
Total Pressure Sizing Method
The total pressure sizing method is a variation of the static regain method. The total pressure of any point in the ductwork represents the actual energy of the moving air at that point. The advantage of this method is that it accounts for all mechanical energy losses in a system. The system design does not have to be dependent on an assumed velocity at the fan outlet.
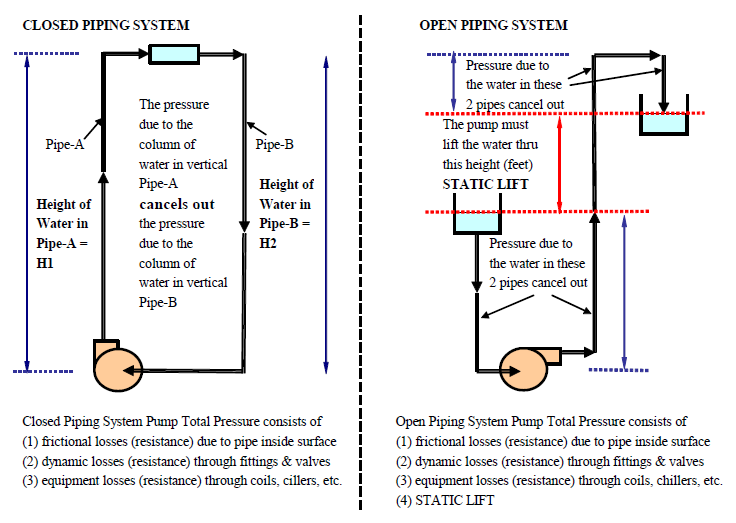
Piping Systems and Networks
Piping systems can be open or closed. An open system is affected by atmospheric pressure. The flow in open condensate return and plumbing drainage systems is gravitational. The flow in an open cooling tower water system is forced. The pipe sections of an open network system are either all supply or all return. A closed network system includes both supply and return sections.
Open Network Systems
Pumps and static heads are used to force circulation in Open Systems except as noted
- Steam supply
- Open steam condensate return (gravitational)
- Closed condensate return
- Cooling tower water (partially gravitational)
- Fuel oil supply
- Fuel oil return
- Gasoline supply
- Fuel gas supply
- Domestic cold water supply
- Domestic hot water supply
- Storm sewer return (gravitational)
- Sanitary sewer return (gravitational)
- Sanitary vents (gravitational)
Closed Network Systems
Closed systems apply mainly to liquids. Examples of closed network systems include
- Chilled water
- HVAC hot water
- High temperature hot water
- Glycols, Brines
Supply-Return Systems
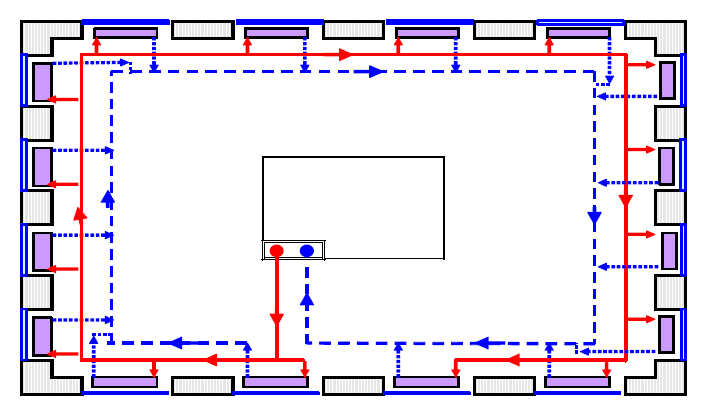
The flow arrangements in closed piping networks can be:
- Two-pipes, direct-return
- Two-pipes, reverse-return
- Primary-secondary
Primary-Secondary Systems
Network arrangements can be combinations of direct return and reverse return loops.

Pipe and Duct Sizing using Charts
The flow (water or air) quantities in the pipe and duct sections are established by the room heating and cooling loads. For example:
Room Sensible Heat Gain (SHG) in summer = 216,000 btu hr
Room Temp (Tr) = 75oF, Ducted Supply Air Temp (Ts) = 55oF
Supply Air CFM = SHG / [ 1.08 * ( Tr - Ts ) ] = 216,000 / [ 1.08 * ( 75 - 55 ) ] = 10,000.
Room Sensible Heat Loss (SHL) in winter = 500,000 btu hr. Room Temp (Tr) = 75oF,
Radiator: Entering Water Temp (EWT) = 200oF. Leaving Water Temp (LWT) = 180oF.
Supply Water GPM = SHL / [ 500 * ( EWT - LWT ) ] = 500,000 / [ 500 * ( 200 - 180 ) ] = 50.
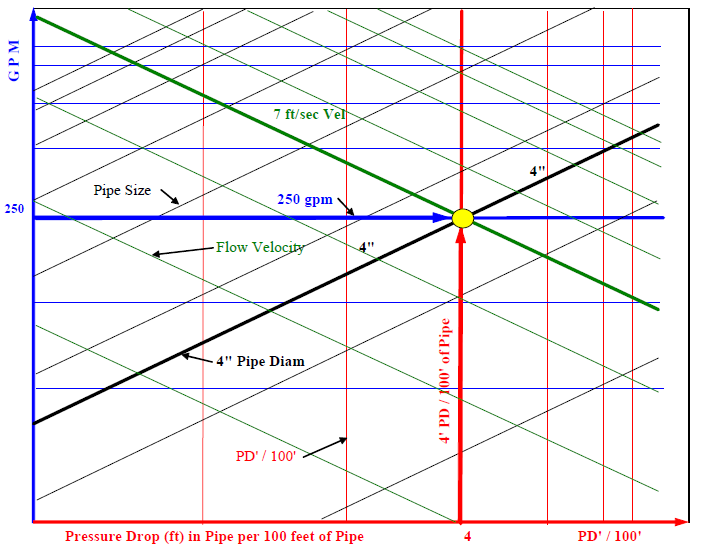
Example: Below is the format of a duct (round) or pipe sizing chart. In this particular case it is a pipe sizing chart. The flow through the pipe is 250 GPM. What is the pipe size in inches and flow velocity in feet per second (FPS) if the pressure drop (ft) per 100 ft of pipe must not exceed 4.0. From the chart the pipe size is 4 inches and the velocity is 7 FPS.
| Pipe Sizing CriteriSchedule 40 Steel | S-40 Steel |
Design: 3'/100' PD , 10 fps max vel High: 5'/100' PD , 12 fps max vel Maxim: 7'/100' PD , 15 fps max ve
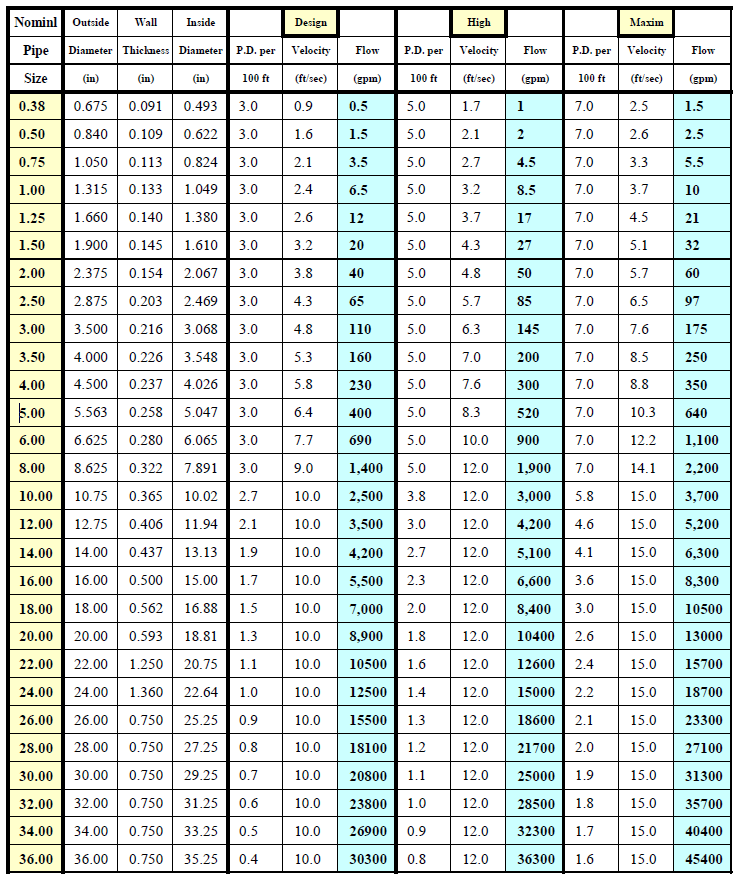
Water Distribution Piping Systems Analysis
The following is a summary procedure for designing a piping distribution system.
Supply and return water quantities for each room have to be calculated first based on heating and cooling loads. GPM = SHL (or SHG) / [ 500 * ( EWT - LWT ) ]
Establish the design criteria limits for designing the water distribution system. This includes:
(1) Pressure drop per length of pipe, (2) Maximum velocity limit.
Locate the terminal devices (radiators, fan-coil-units, etc.) in the rooms and assign the calculated room water flow quantities to them.
Route piping from the pumps to the terminal devices.
Determine the water flow quantities in each pipe section.
Size the piping based on the design criteria (low, medium or high pressure/velocity systems).
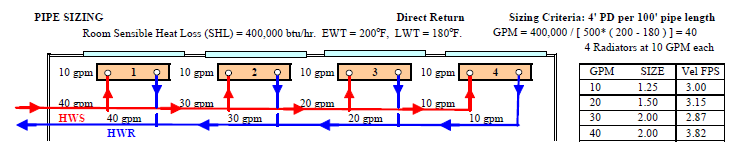
Pipe Sizing Examples
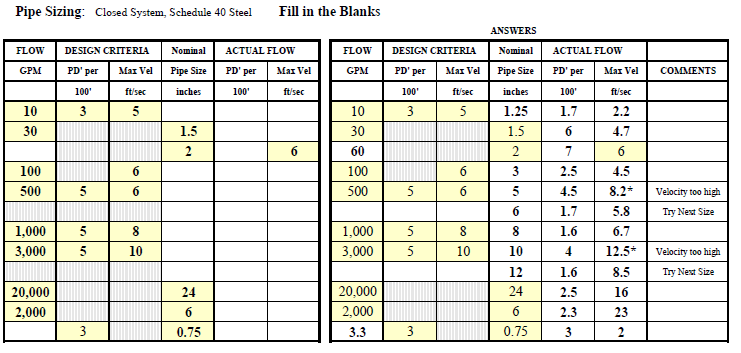

Air Distribution Ductwork Systems Analysis
The following is a summary procedure for designing an air distribution system.
Supply or extract (return and exhaust) air quantities for each room have to be calculated first based on heating and cooling loads and indoor air quality standards. CFM = SHG / [ 1.08 * ( Tr - Ts ) ]
- Establish the design criteria limits for designing the air distribution system. This includes:
(1) Sizing method and associated velocity limits, (2) Ductwork dimensional criteria, (3) Static and total pressure limits to be used in selecting fans and sizing ductwork. - Locate the terminal devices (diffusers, registers and grilles) in the rooms and assign the calculated room air quantities to them.
- Route ductwork from the fans to the terminal devices.
- Determine the air quantities in each duct section.
- Size the ducts based on the design criteria (low, medium or high pressure/velocity systems).

- Calculate the pressure drop in each duct section. This consists of frictional losses in the ductwork and dynamic losses in the fittings (bends, splitters, dampers, etc.). A duct section has a constant air quantity, constant velocity (size does not change) and constant shape (round, rectangular or oval). A new section is created when one of these factors change

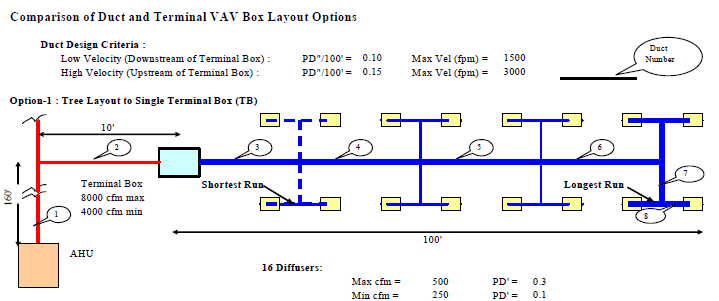
Duct Sizing Examples
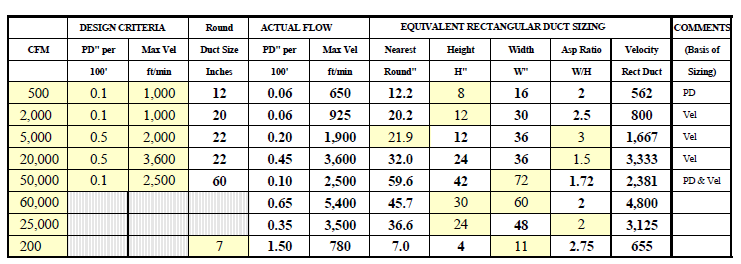
Duct Sizing : Galvanized Steel Fill in the Blanks
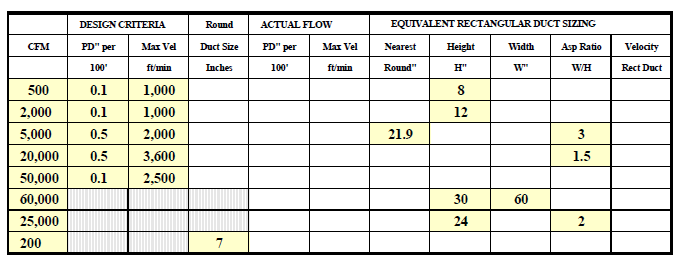
Answers Note: Rectangular Duct Velocity (fpm) = (CFM x 144)/(W x H)
AHU : Air Handling Unit