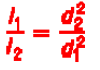Lighting (NASA)
Light consists of electro-magnetic waves. It is the segment of the electro-magnetic spectrum of radiant energy that lets us see. All radiant energy consists of electro-magnetic waves traveling at what we commonly call the "speed of light". The speed of light in a vacuum or air is 300 million meters per second approximately or 186 thousand miles per second. In water it is 225 million meters per second and in glass it is 200 million meters per second. Radiant energy is one form of energy. The other forms of energy include chemical, electrical, thermal, kinetic and atomic.
Lighting design is possible because light is predictable. It obeys the laws of physics and exhibits fixed characteristics. Lighting design is a creative and subjective science because it also involves aesthetics. The primary objective is to provide the right amount of light for a given task.
Light as a Wave
 The quantity that is "waving" is the electromagnetic field, an esoteric but quite measurable entity: your lights shine and your microwave runs and your radio plays because the electromagnetic field exists. As illustrated in the adjacent image, a wave has a wavelength associated with it.
The quantity that is "waving" is the electromagnetic field, an esoteric but quite measurable entity: your lights shine and your microwave runs and your radio plays because the electromagnetic field exists. As illustrated in the adjacent image, a wave has a wavelength associated with it.
It is normal to give the wavelength of light the symbol Greek "lambda". Some common units of length employed for wavelengths of electromagnetic radiation are summarized in the following table. (The micrometer is often still called by its old name, the micron.)
The speed of light in a vacuum is commonly given the symbol c. It is a universal constant that has the value. c = 3 x 108 meters/second. The speed of light in a medium is generally less than this. Normally the term "speed of light", without further qualification, refers to the speed in a vacuum.
| Vacuum: c = 299,792,458 meters/second. Water: c = 225,407,863 meters/second. | Air: c = 299,702,547 meters/second. Glass: c = 199,861,638 meters/second. |
A wave can be characterized by its wavelength, but we can also characterize it by the frequency (how many wavelengths pass a fixed point in a given time; think of sitting on the dock---of the bay---counting the number of water waves passing in one minute) and the energy that it carries. For light waves the relationship among the wavelength (usually denoted by Greek "lambda" meters), the frequency ("f" cycles per second), and the speed of light ("c" meters/second)
λ = c /f
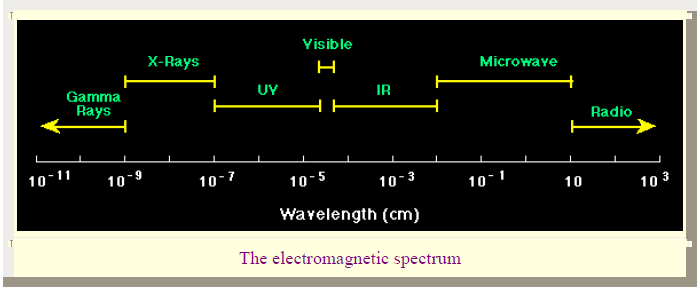
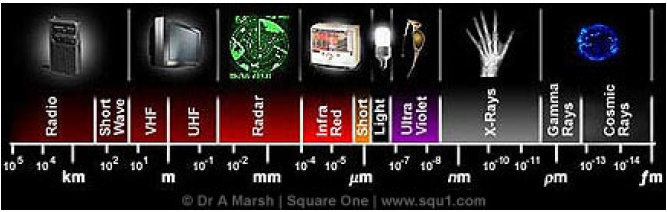
The Electromagnetic Spectrum
The electromagnetic spectrum is the distribution of electromagnetic radiation according to energy (or equivalently, by virtue of the relations in the previous section, according to frequency or wavelength). The following table gives approximate wavelengths, frequencies, and energies for selected regions of the electromagnetic spectrum. The notation "eV" stands for electron-volts, a common unit of energy measure in atomic physics. A graphical representation of the electromagnetic spectrum is shown in the figure below.
Example: Electrical Power Supply is 60 Hz or 60 cycles per second (f) and the speed of light is 300,000,000 meters per second (c). Wavelength = λ = c / f = 500,000 meters. The wavelength of electricity has no significance
The dividing line between the different forms of electromagnetic wave energy is not sharp as the numbers above might indicate and it is a gradual transition from one form to another. Since wavelength (λ) times frequency (f) is constant, the different energy forms can be expressed in frequency (ex. radio, electricity) or wavelength (ex. radio, gamma rays).
Thus we see that visible light and gamma rays and microwaves are really the same things. They are all electromagnetic radiation; they just differ in their wavelengths. The visible part of the spectrum may be further subdivided according to color, with red at the long wavelength end and violet at the short wavelength end, as illustrated (schematically) in the following figure.
The sequence of colors red, orange, yellow, green, blue, and violet may be remembered by memorizing the name of that fine fellow "ROY G. BV". This was originally "ROY G. BIV", because it used to be common to call the region between blue and violet "indigo". In modern usage, indigo is not usually distinguished as a separate color in the visible spectrum; thus Roy no longer has any vowels in his last name.
Refraction and Diffraction
The wave nature of light leads to two very important properties: refraction, where the direction of light propagation is altered at the boundary between media of different densities, and diffraction, which has among its consequences that light can "bend around corners". action of Light
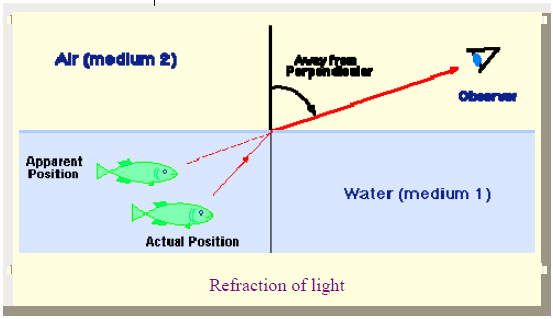
The direction of light propagation can be changed at the boundary of two media having different densities. This property is called refraction, and is illustrated in the following figure for the boundary between air and water.
The apparent and actual positions of the fish differ because the direction of light propagation has been changed as light passes from the more dense water into the less dense air.
If we adopt the convention that the light passes from medium 1 into medium 2, the general rule is that the refraction is
- Away from the perpendicular if medium 2 is less dense than medium 1
- Toward the perpendicular if medium 2 is more dense than medium 1
 Thus, in the above example the refraction is away from the perpendicular because air is less dense than water. Such effects form the basis of the refracting telescope, and of optical devices using lenses in general. Because light is a wave, it has the capability to "bend around corners". This is called diffraction, and is illustrated in the adjacent image. The intensity of light behind the barrier is not zero in the shadow region. diffractive effects occur generally when a part of a light wave is cut off by an obstruction.
Thus, in the above example the refraction is away from the perpendicular because air is less dense than water. Such effects form the basis of the refracting telescope, and of optical devices using lenses in general. Because light is a wave, it has the capability to "bend around corners". This is called diffraction, and is illustrated in the adjacent image. The intensity of light behind the barrier is not zero in the shadow region. diffractive effects occur generally when a part of a light wave is cut off by an obstruction.
Intensity: the Inverse Square Law
The intensity of light observed from a source of constant intrinsic luminosity falls off as the square of the distance from the object. This is known as the inverse square law for light intensity.
Thus, if I double the distance to a light source the observed intensity is decreased to (1/2)2 = 1/4 of its original value. Generally, the ratio of intensities at distances d1 and d2 are
END of NASA Text
The Characteristics of Light
Light exhibits a range of behavioral characteristics common to all other wave and wavelike phenomenon. These fall into the following categories:
- Transmission or Transmissivity
- Reflection or Reflectivity
- Refraction
- Diffraction
Lighting Laws
- Inverse Square Law
- Cosine Law
Building materials such as brick and concrete, transmit, reflect and absorb radiant wave form energy in varying degrees. The absorbed portion is eventually transmitted to the surrounding space by conduction and convection.
In the case of light, which is also part of the wave form energy spectrum, absorptance or absorptivity is insignificant and can be ignored.
Transmission
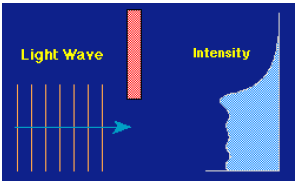
Light transmission property of a building material such as glass is measured as the ratio of the amount of light that is transmitted to the total incident light falling on the glass surface. This property factor of glass is called transmittance. In general transmittance should only be applied to materials that transmit the various component colors of light equally.
A sheet of clear glass and a sheet of frosted glass might both have a transmittance value of 0.5 but they affect the incident light differently. Transmittance is the ratio of transmitted light to total incident light on the surface.
Reflection
Reflection property of building materials is measured as the ratio of the amount of radiant energy that is reflected to the total incident radiant energy falling on the surface. This property is called reflectance. Black solid opaque objects will absorb a significant amount of the radiant energy whereas a polished silver surface will reflect most of it away.
The reflectance properties of the inside surfaces of a space and of the objects in the space affect lighting and daylighting of the space. Reflectances of surfaces have both negative (glare) and positive (reduced lighting energy) impacts on the space. In the case of windows, reflective glass can have a negative affect on other buildings and street conditions but on the positive side it reduces radiant cooling energy.
Specular Reflection (or Reflection) is observed on a smooth polished surface. The angle of the reflected light is equal to the angle of incident light. Diffuse reflection occurs on a rough surface. The reflected light is scattered in all directions. Most surfaces are a combination of specular and diffuse reflections. Reflectance is the ratio of reflected light to total incident light on the surface.
A Lambertian surface reflects (diffuse reflection) light or radiation equally in all directions. An example of a Lambertian surface would be very fine reflective powder such as talcum or flour.

Refraction
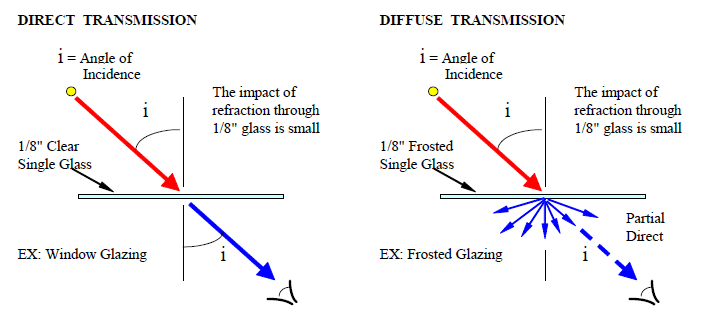
Refraction is an effect that occurs between transparent materials of different densities. The transparent material might be a gas (air), liquid (water) or solid (glass).
The bending effect in the refraction phenomenon is a physical representation of the longer time it takes for light to move through the denser of the two materials and it is dependent on the angle with which the ray of light strikes the boundary surface.
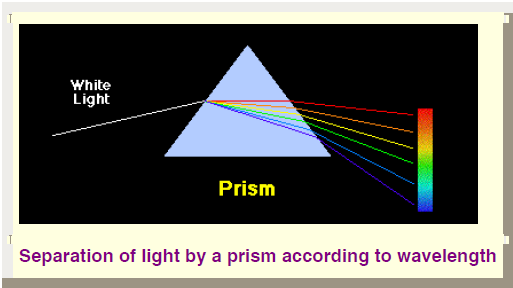
When light passes through dissimilar materials, the rays bend and change velocity slightly. This effect is called refraction. The refractive index is constant for a given transparent material. However, different wavelengths of light representing the colors (red, orange, yellow, green, blue, indigo and violet) have slightly different refractive indices when they pass through certain materials such as a quartz prism. A material such as a quartz prism can therefore separate the colors of light when it passes through it.
| Medium | Speed of Light | Refractive Index |
| Air | 299,702,547 m/s | 1.0 |
| Water | 225,407,863 m/s | 1.333 |
| Glass | 199,861,638 m/s | 1.517 |
| Diamond | 2.417 |
Diffraction
Diffraction is another wave phenomenon that is dependent on wavelength. Light waves appear to bend as they pass by the edge of a plane or a narrow opening or slit. The effect is negligible in the case of building lighting design.
Sources of Light
| Natural: | (1) sun, (2) moon - reflected light from the sun, (3) stars, (4) lightning, (5) thermo-luminescence - glow from hot materials, (6) bio-luminescence - fireflies. |
| Artificial: | (1) incandescent - by heating filaments to high temperatures, (2) gaseous discharge - gas atoms of a substance excited to high energy levels by electron collisions will radiate (or glow) when they return to normal state |
Light and Color
White light is a combination of the wavelengths throughout the visible spectrum and that each of these wavelengths is associated with a separate color (Red, Orange, Yellow, Green, Blue, Indigo, Violet - ROY G BIV). The colors of the visible spectrum range from red (the longest wavelength of the visible spectrum, 780 nanometers) to violet (the shortest wavelength, 380 nanometers). If all wavelengths of the visible spectrum are combined at approximately equal power levels the result is white light. An example of this is natural sunlight.
Every object has a unique spectral response characteristic. This property determines the color of the object, and in combination with the color spectrum of the light source, determines the colors that we see. Light from the source strikes an object and is reflected, transmitted, or absorbed. If the color of the object is present in the light source, the wavelength of light corresponding to the color of the object is reflected to the human eye and we see that particular color. The remaining colors in the light source are transmitted or absorbed.
In order to see the color of the object, the light striking the object must contain the color of the object. For example, a red apple illuminated with green light will appear black because the red wavelength is absent in the green light source. Since white light consists of all the colors, we can see objects of different colors.

Traffic lights have Red, Yellow and Green transparent glass lenses. A light is projected from behind the glass lens through the glass so that you can see the color in pitch darkness. If the traffic light is painted on the outside in Red, Yellow and Green, then it cannot be seen in pitch darkness unless you shine your headlights on to it.
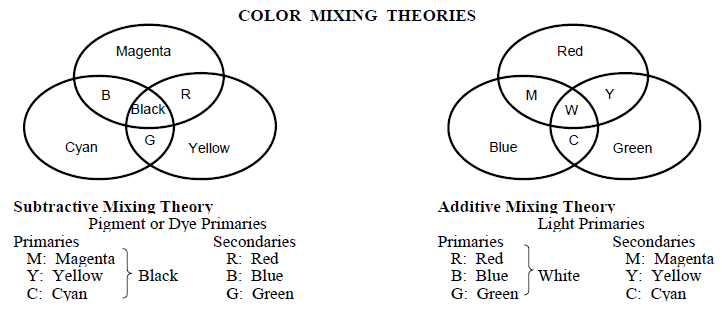
The colors that we see are explained by several theories of color mixing. When dealing with pigments or dyes there are three colors that can be mixed to form other colors of the visible light spectrum. These three colors, referred to as the subtractive primaries are Magenta, Yellow and Cyan. By mixing parts of these, the subtractive secondaries of Red (magenta + yellow), Blue (magenta + cyan) and Green (cyan + yellow) are formed. The mixture of all three primaries (magenta + cyan + yellow) results in Black or the absence of color.
The additive color mixing theory deals with the mixing of light. Red, Blue and Green additive light primaries can be paired to form Magenta (red + blue), Yellow (red + green) and Cyan (green + blue). When all three primaries are combined the result is White light.
Example: A transparent plastic sheet transmits 40% of the lumens per sq.ft. of incident light incident (that falls) on its surface. The amount of light absorbed is insignificant (0%). If 50 lumens per sq.ft. are incident on its surface how much is transmitted and reflected?
Transmittance of plastic = 40% = 0.4
Transmitted lumens = 0.4 * 50 lumens = 20 lumens.
Absorbed lumens = 0%
Reflected lumens = Total - (transmitted + absorbed) = 50 - 20 = 30 lumens.
Sum of Transmittance + Absorptance + Reflectance = 1 0.4 + 0.0 + R = 1. R = 1 - 0.4 = 0.6
Reflected lumens = 0.6 * 50 lumens = 30 lumens.
Properties of Glass ( Average / Typical )
| Glass Type | U | SHGC | SC | VLT |
| UnitsSingle, Clear | 1.00 | 0.75 | 0.88 | 0.90 |
| Single, Tinted | 1.00 | 0.64 | 0.75 | 0.80 |
| Double, Clear | 0.60 | 0.66 | 0.78 | 0.80 |
| Double, Tinted | 0.60 | 0.55 | 0.65 | 0.65 |
U = Heat Transfer Units
SHGC = Solar Heat Gain Coeff.
SC = Shading Coeff.
SC = SHGC / 0.85 approx.
VLT = Visible Light Transmittance
U & SHGC from International Energy Conservation Code (IECC)
Increasing Daylighting Effectiveness
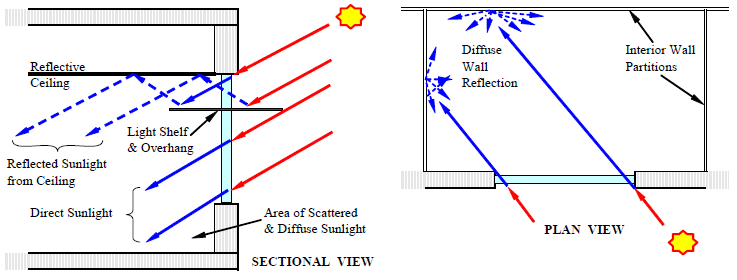
Lighting Design
The objectives of lighting design are to provide the right amount and quality of light for different tasks and ensure the lighting is energy efficient. Lighting design factors that can be controlled include:
- Direction
- Quantity and Uniformity
- Color
Direction
Direction can enhance and emphasize an objects perceived shape or form.
Fill lighting (or flood lighting) is multi-directional light. It reduces shadows on an object.
Key lighting is directed from a single point source. It produces bright areas and shadows.
Grazing lighting is achieved by directing the light at a surface from a narrow angle. Grazing enhances variations in surface depth revealing texture.
Silhouette lighting is achieved by directing the light against the background and not the object itself. The object is seen as a dark outline against a bright background.
Up-light technique places a light source below an object. It produces shadows that are reversed from how an object is shadowed with daylight.
Each of these techniques can have an impact on how the final object appears.
Quantity and Uniformity
Technically the eye does not see light striking a surface. The eye only sees transmitted or reflected light. However the quantity of light is commonly used in describing lighting levels. The eye's sensitivity to light is not a linear scale. A doubling of light levels with say two 100 watt lamps will not make an object appear twice as bright. The eye processes light logarithmically.
The uniformity of illumination describes how evenly light spreads over an area. Creating uniform lighting requires proper luminaire spacing. Typically, a floor would have low uniform general lighting over the entire floor space and higher uniform task lighting for specific tasks in order to save in lighting energy and costs.
Color Metrics
Color can be described using a variety of metrics. The two most common measuring metrics are Correlated Color Temperature (CCT) and Color Rendering Index (CRI).
Correlated Color Temperature (CCT)
CCT is the metric through which source light (lamps & fixtures) is specified. This metric measures light sources as being of different "whiteness". Some sources, like incandescent lamps, have a yellowish white appearance, while others like daylight have a bluish white appearance. The temperature specification system measures or quantifies the degree of whiteness.
CCT is expressed using the Kelvin temperature scale where oK = oC + 273. A lower CCT means longer wavelengths and "warmer" color. An example is a conventional electric stove element which glows bright red when the unit is on high temperature. Actually this is a low temperature on the CCT scale. If the temperature of the element was increased to much higher levels, the light emitted would appear more white than red. As the temperature is increased further, the metal would emit a bluish white light and it would appear blue at much higher temperatures. Typical CCT values for light sources vary from 2100 oK to 6500 oK.
CCT can influence the atmosphere of a room. Laboratories and grocery stores generally use cool bluish white sources such as fluorescent lamps while restaurants try to provide a warm yellow-orange-red color similar to that from candles.
Color Rendering Index (CRI)
The color appearance of a surface is the result of both the wavelengths present in the light source and the extent to which each of these wavelengths are reflected from the surface. A green surface reflects mainly the green range of wavelengths. There can be a variety of green colors depending on the specific band of wavelengths that are reflected.
Color Rendering Index (CRI) is a metric used to evaluate a CCT of a light source based on how well they render the colors of an object compared to a standard source of light at the same CCT. The standard source is selected as having excellent color rendering at that color temperature or CCT. CRI values range from 0 to 100. The higher the number, the easier to distinguish colors. A CRI > 75 provides good color rendition and a CRI < 55 provides poor color rendition.
Daylight and Color
Daylight has excellent color rendering ability. Daylight is used as the standard illuminant against which electric light sources with CCT greater than 5000 oK are compared to determine the CRI. Daylight, when the sun is at a high altitude, is considered to have a CRI of 100. At lower altitudes sunlight has a reddish color.
CCT and CRI of Artificial Light Sources
Incandescent light sources, which include tungsten halogen sources, are generally good color rendering sources. They are smooth in light distribution and contain all the wavelengths of the light spectrum. Incandescent sources typically have a CRI that is close to 100. Tungsten halogen sources have a slightly higher CRI and color rendering ability than standard incandescent because of the higher filament temperatures obtained.
Fluorescent light sources vary in color rendering ability. The standard cool white lamp, which has been used in most offices in the past, has a color temperature (CCT) of about 4200oK and a color rendering ability (CRI) of about 62. In recent years, lighting manufacturers have produced lamps that utilize phosphors that provide both better color rendering and increased light output.
High Intensity Discharge (HID) light sources fall into three categories:
- Mercury
- Metal Halide
- High Pressure Sodium
Each of these lamp types offers a range of color temperatures (CCT) and color rendering qualities (CRI). Mercury lamps are becoming less popular because of their lower efficacy (lumens/watt) and poor color rendering ability. CRI varies from 15 to 30
Metal halide lamps, in general, provide good color rendering since they emit light at many different wavelengths. Within this family of lamps, there are many variations in color rendering ability (CRI 60 to 90). Metal halide lamps change in color temperatures over their life time. For this reason groups of lamps must be replaced together to maintain consistent color quality.
High pressure sodium lamps are generally poor in rendering quality but have high efficacies and longer lives (CRI = 20). For this reason they are used mainly for exterior applications. Low pressure sodium lamps provide mainly monochromatic light at about 589 nanometer wavelength (CRI less than 0). It is used for roadway and outdoor/indoor car parking lighting.
Within the lighting industry there are many different white light sources. In most cases, these sources do not appear as equal power white light, but instead are tinted slightly, usually in either the red or blue direction. The "warmness" of the light (incandescent associated with red, orange & yellow) or “coolness” of the light (gas discharge associated with blue, indigo), depends on the relative amounts of the colors it produces.
| Light Source | Lumens | Lumens | CCT | CRI |
| per Watt | ||||
| 100 watt incandescent | 1,750 | 18 | 3,000 | 98 |
| 100 watt tungsten halogen | 1,880 | 19 | 3,200 | 100 |
| 40 watt fluorescent | 3,150 | 79 | 3,400 | 57 |
| 175 watt metal halide | 14,000 | 80 | 3,700 | 60 |
| 150 watt high press sodium | 16,000 | 107 | 2,100 | 21 |
The Five Lighting Metrics
As with distances measured in feet or meters, weights measured in pounds or kilograms, and heat measured from a traditionally chosen reference point with measuring scale units that are set arbitrarily, lighting has it's own terminology and measuring scales. Fortunately in lighting, there are only five basic metrics (measuring systems) that need to be learned. Unfortunately they have similar names and unusual units that make it difficult for beginners to master.
| Metric | Symbol | English (IP) Units | Metric (SI) Units | Comments |
| Luminous Flux | F | Lumens | Lumens | Light Flow Quantity |
| Luminous Intensity | I | CandlePower or Candela | Candela | Light Production |
| Illuminance | E | Lumens/Sq.Ft., FootCandles | Lumens/Sq.M., Lux | Light Received |
| Luminance | L | Candelas / Sq.Ft. | Candelas / Sq.M. | Reflected - Intensity |
| Luminous Exitance | M | Lumens / Sq.Ft. | Lumens / Sq.M. | Reflected Illuminance |
(1) LUMINOUS FLUX (F)
Luminous flux is a measure of the flow of light quantity. The flow quantity is measured in lumens. A common analogy is the flow of water through a shower head (flashlight). The shower head could be a spherical ball (round light bulb) perforated with holes with water being forced through it radially outwards in all directions as a spray fountain. The water spray will eventually bend towards the ground due to gravity, whereas light will continue to travel in a straight line. Another analogy would be the magnetic field around a magnet.
An incandescent lamp is shown in the figure below. The lamp's filament receives an electric current making it to glow with light or emit luminous flux. The construction of the lamp bulb as a sphere is to try and make the light flow equally in nearly all directions. The incandescent lamp shown receives electrical energy in watts which is used by the lamp to generate light measured in lumens. The measure of the lamp's success in converting electricity to light is called efficacy.
Efficacy of a lamp is the ratio of the lumens (of light) it emits to the amount watts (of electricity) that it uses. The unit of efficacy is lumens/watt.
(2) LUMINOUS INTENSITY (I)
Luminous Intensity is a measure of the force generating the luminous flux (light). It is analogous to pressure in fluid system that forces flow through the piping or ductwork system and voltage in an electrical system that forces current flow through the conductor. The force generating the light depends on the light source only and it is independent of the visual senses that see the light and the objects that the light falls on and the reflected light from the object.
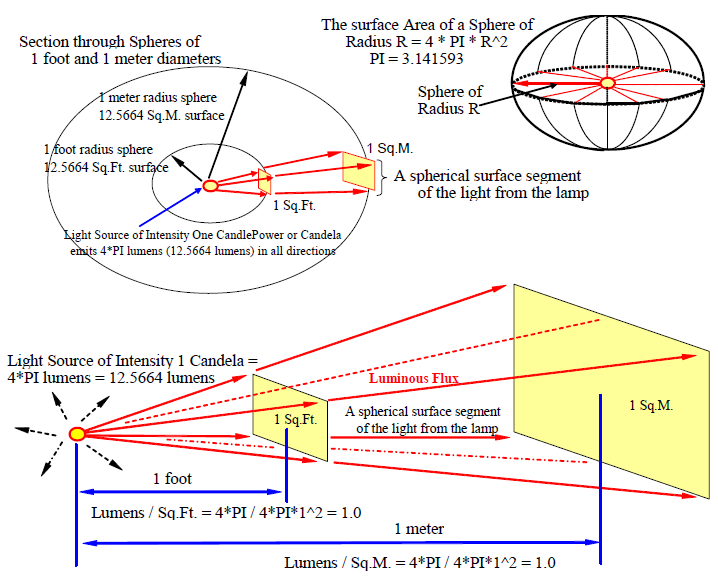
The measuring unit for luminous intensity is the Candela (English and Metric units). The original English unit name was CandlePower (CP). As with HorsePower (HP), one candlepower represented the light from one standard candle. By definition, One Candela (or CandlePower) generates 4*PI lumens of light spherically and equally in all directions. (PI = 3.141593). One candela emits 12.56637 lumens.
Since the surface area of a sphere is 4*PI*R2, and the total lumens emitted by one candela is 4*PI, the lumens of light falling on a surface at a distance of R feet is 1/ R2 lumens per square foot and at a distance of R meters is 1/ R2 lumens per square meter.
The lumens of light from 1 Candela intensity falling on a surface at a distance of 1 foot is
= 1/ 12 lumens per square foot = 1 lumen per square foot
The lumens of light from 1 Candela intensity falling on a surface at a distance of 1 meter is
= 1/ 12 lumens per square meter = 1 lumen per square meter
Definition of Lumen
A light source of 1 Candela Intensity produces 1 Lumen / Sq.Ft. at a distance of 1 Foot.
A light source of 1 Candela Intensity produces 1 Lumen / Sq.M. at a distance of 1 Meter.
The definition of Lumen is therefore derived indirectly from Luminous Intensity. The definition of the units for Luminous Intensity (Candela) was arbitrarily set as 4*PI Lumens per Candela.
(3) ILLUMINANCE (E)
The source of light that produces light has Luminous Intensity which is measured in Candelas. The amount of light that flows or is transmitted from the source is called Luminous Flux and is measured in Lumens. As luminous flux travels outwards from the surface it ultimately impinges or falls on an object or surface where it is reflected, absorbed or transmitted. We need to know the amount or strength (density) of light reaching the surface to perform various tasks such as reading.

Illuminance is a measure of the amount of light falling on a surface. The measuring units are Foot Candles (Lumens per Square Foot - English units) and Lux (Lumens per Square Meter - Metric units). E (Illuminance) = F (Luminous Flux in Lumens) / A (Surface Area). E = F/A.
| Since | 1 square meter = 10.764 square feet and 1 square foot = 0.0929 square meters, |
| 1 lumen/m2 (Lux) = 1 lumen/10.764 ft2 = 0.0929 lumens/ft2 (FootCandles) | |
| 1 lumen/ft2 (FootCandle) = 1 lumen/0.0929 m2 = 10.764 lumens/m2 (Lux) |
So 1 FootCandle is almost 11 times greater than 1 Lux.
Example: 900 lumens (F) from a light source fall on (reach) a desk that is 5' x 3'. The Illuminance (E) at the desk is = 900 / (5 x 3) = 60 lumens per square foot = 60 FootCandles.
Inverse Square Law
The three metrics (Flux, Intensity and Illuminance) discussed so far are related. Consider a light source with an intensity of 100 Candelas in the direction (not spherical) of three surfaces. The light from the source reaches three surfaces at a distance (D) of 1, 2 and 3 feet and the areas (A) of the surfaces are 1 (1' x 1'), 4 (2' x 2') and 9 (3'x3') square feet.
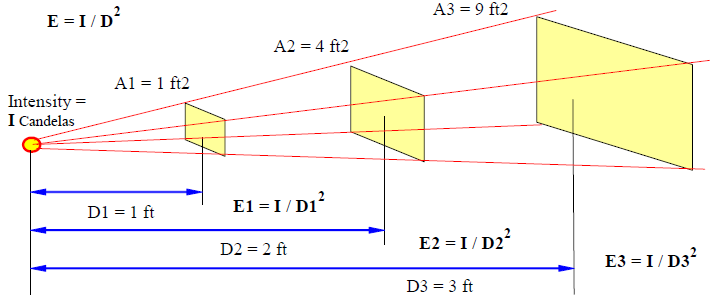
By definition, one candela light source radiates one lumen to a one square foot spherical surface one foot away. Therefore the 100 candela light source will send 100 lumens to each of the 3 surfaces and the Illuminance on each surface will be 100/1 = 100 FC on A1; 100/4 = 25 FC on A2; and 100/9 = 11 FC on A3. From this a general equation can be formed.
E = I / D2
Illuminance on a surface = Intensity of the light from the source directed at the surface divided by the square of the distance of the surface from the light source. This is known as the Inverse Square Law. It says that the Illuminance from a small source of light is directly proportional to the intensity of the source and inversely proportional to the square of the distance between the light source and the surface receiving the light.
The Illuminance on A2 is one-fourth of A1 and on A3 is one-ninth of A1. If the intensity of the light source were doubled to 200 candelas, then the illuminances on A1, A2 and A3 would also double to 200, 50, and 22 footcandles respectively.
Cosine Law
The amount of light (say 100 units) falling on a surface depends on the angle that the ray of light makes with the surface. An oblique angle spreads the 100 units over a greater area. If the light is directed perpendicular to the surface then the 100 units falls on the minimum surface possible.
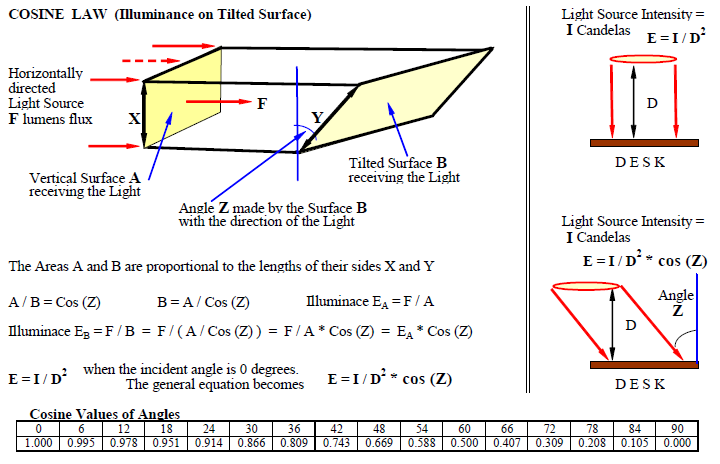
Example: 500 Candelas of light (Intensity I) is directed at a surface that is 6 feet (D) away. The surface is tilted away from the direction of the light source at an angle of 30 degrees (Z). What is the Illuminance (E) on the surface?
E = ( I / D2 ) * Cos (Z) = ( 500 / (6*6) ) * Cos (30) = 13.89 * 0.866 = 12 Foot-Candles.
Example: A 40 watt, 48 inch fluorescent light tube fixture produces 4000 lumens of light directed uniformly over a floor 10' x 10'. The overall efficiency of the light fixture is 50%. What is the illuminance (E) on the floor? What is the lamp Efficacy?
Useful luminous flux (F) reaching the floor = 4000 * 0.5 = 2000 lumens. Floor area = 100 sq.ft.
Illuminance (E) = 2000 / 100 = 20 Foot-Candles (lumens / sq.ft.)
Illuminance (E) = 20 FC * 10.764 sq.ft. per sq.m. = 215.28 Lux (lumens / sq.m.)
Lamp Efficacy = 2000 lumens / 40 watts = 50 lumens/watt.
Example: 2000 lumens (F) reach a floor 10' x 10' (A1) that is 20 feet (D1) from the light source. What is the illuminance at a distance 10 feet and what is the surface area covered by the light?
E1 = F / A = 2000/100 = 20 FC = I / (D1*D1) = I / (20*20) = I / 400
E2 = I / (D2*D2) = I / (10*10) = I /100
E2 / E1 = 400 / 100 = 4
E2 = E1 *4 = 20 FC * 4 = 80 FC (lumens / sq.ft.)
Area A2 = 2000 lumens / 80 FC = 25 sq.ft. or A1 / A2 = 4 A2 = A1 / 4 = 100/4 = 25 sq.ft.
Example: A flood light source of intensity 9000 candelas (I) is aimed at a point P that is at 30 feet distance horizontally and 20 feet distance vertically. What is the illuminance (E) at point P?
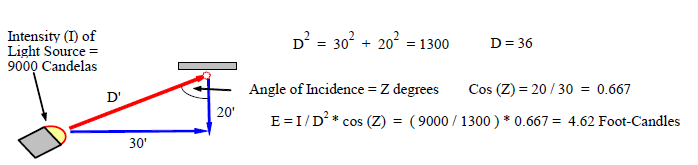
Recommended Illuminance Levels

Luminous Intensity refers to the total amount of light emitted from a light source. For example, 100 candelas or candlepower can be emitted by a light source with a spherical surface area of 100 square inches or 10 square inches. It is independent of the viewer (independent of the distance and direction relative to the viewer). One candela emits 4*PI (12.57) lumens.
Luminous Flux is the amount of light measured in lumens transmitted from a light source to an object or surface. It is independent of the viewer. The viewer does not see the quantity of light being transmitted.
Illuminance is the amount of light in lumens falling on an object or a surface area. It is also independent of the viewer. The viewer does not see the lumens per square foot (footcandles) or lumens per square meter (lux). Not all the lumens leaving the light source will fall on the surface.
The remaining two lighting metrics, Luminance and Exitance are related to the viewer.
The Luminance of a source or surface is the reflected Intensity from a surface in the direction of an observer divided by (dependant on) the surface area of the reflected light source as seen by the viewer. The units are therefore candelas per square foot or candelas per square meter.
The Exitance of a source or surface is the reflected Illuminance from a surface in the direction of an observer divided by the surface area of the light source seen by the viewer. The units are lumens per square foot or lumens per square meter.
(4) LUMINANCE (L)
Luminance is an objective physical quantity that is often confused with brightness. The quantity is the same for all viewers. Brightness is a subjective evaluation or interpretation of the amount of light reaching the visual system. What is considered bright by someone with sensitive eyes might be normal to others although the intensity of light from the object is the same to all viewers.
The visual system sees luminance, the energy reflected from an object. It does not see illumination, the light arriving at the object. The light reaching a surface is not an indication of how well a task can be seen. Seeing is a function of the light leaving a surface or object. Comfort and visibility are dependent upon the luminance of objects and surfaces within the field of vision
The luminance of a source or surface is defined as the intensity of the object or surface in the direction of the observer. Luminous Intensity of the light source is an absolute value that is independent of the observer and the surface area of the source.
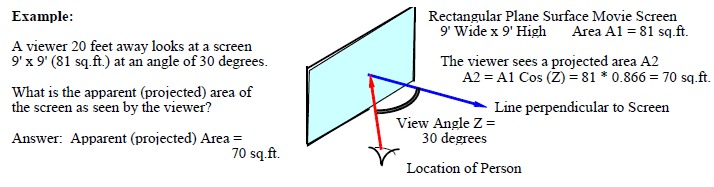
The figure below illustrates luminance. The full face view of the lamp is a circle of diameter D. The face area A = PI * D^2 / 4. In the first example the eye sees the full face area of the lamp. In the second case the eye sees the face of the lamp at an angle and sees an elliptical (reduced in one direction) surface with an area A = A*Cos(Z) where Z is the view angle.

The units of Luminance are:
Candelas per square meter (Metric / SI)
Candelas per square inch OR Candelas per square foot (English / IP)
One Candela per square inch = 1550 candelas per square meter
One Candela per square inch = 11 candelas per square foot
Example: The luminous Intensity (Ix) measured directly perpendicular (0 degrees angle) to the face of a lamp is 5000 candelas. The Intensity measured at an angle of 30 degrees to the perpendicular is 3000 candelas. The circular face of the lamp has an area of 20 square inches. What is the Luminance (L) seen by the observer at the two positions x and y?
Lx = 5000 / 20*Cos(0) = 5000/20 = 250 candelas/in2 = 388,000 candelas/m2
Ly = 3000 / 20*Cos(30) = 3000/20*0.866 = 173 candelas/in2 = 268,000 candelas/m2
Note if the Intensity (I) of the lamp (half or full sphere bulb) had been the same in direction x and y, then Ix = Iy = 5000 candelas. However the face area of the lamp seen by the observer would be the full circle of 20 in2 in the case of Ix and 17.3 in2 in the case of Iy.
Luminance (L) = Intensity (I) / A * Cos(Z) L = I/A for Z = 0 degrees (direct view)
I is the light intensity at the point of observation and A * Cos(Z) is the projected surface area of the lamp seen by the observer. When viewed directly, the angle Z = 0 degrees and Cos(Z) = 1.
Example: 1700 lumens of light are emitted equally in all directions from a 100 watt spherically shaped light bulb. The diameter of the bulb is 6 cm (2-3/8 inches). What is the luminous intensity (I) and luminance (L)?
1 candela generates 4*PI lumens spherically. How many candelas would generate 4*PI lumens?
Intensity (I) = F / A-sphere = 1700 / 4*PI = 135.28 candelas.
The projected area A of light is a circle of diameter D = 6 cm (0.06 m) = PI * D^2 / 4 =
3.1416 * (0.06)^2 / 4 = 0.0028274 m2.
Luminance (L) = I / A-circle = 135.28 / 0.0028274 = 47,846 candelas / sq.m.
This is a potential source of glare.
Example: Because of the glare in the previous example, enclose the light bulb in a glass globe of 20 cm (0.2 m) diameter with a light transmittance value of 30%. What is the luminance?
The viewer sees the light coming from a circular section of the outer glass globe of diameter 0.2 meters and only 35% of the lumens leaving the inside light bulb leave the outside globe. This reduces the intensity by 35%.
I = 135.28 candelas * 0.35 = 47.35 candelas.
Projected circular surface area of sphere = PI*D^2/4 = 3.1416 * (0.2)^2 / 4 = 0.03142 sq.m.
L = I / A = 47.38 / 0.03142 = 1507 candelas / sq.m.
(5) LUMINOUS EXITANCE (M)
The fifth metric also describes luminous flux (lumens) leaving a surface or object but it is not directionally dependent. The concern is not the luminance in a particular direction but with the total amount of lumens transmitted or reflected from a surface or object. An insignificant portion of the light energy can be assumed to be absorbed.
Exitance (M) is the luminous flux (F) reflected (Mr) or transmitted (Mt) by a surface area (A). The units are lumens per square foot which is the same as Illuminance.
Illuminance (E) describes incident flux. Exitance describes departing flux (reflected or transmitted). The units in both cases are lumens per square foot or lumens per square meter.
Fi = luminous flux (lumens) incident on material surface
E = Fi / A lumens/ft2 (foot candles) OR lumens/m2 (lux)
Fr = luminous flux (lumens) reflected from surface
Mr = Fr / A lumens/ft2 (foot candles) OR lumens/m2 (lux)
Ft = luminous flux (lumens) transmitted through material
Mt = Ft / A lumens/ft2 (foot candles) OR lumens/m2 (lux)
Fr = R * Fi where R = reflectance of material Mr = Fr / A = R * Fi / A = R * E
Ft = R * Fi where T = transmittance of material Mt = Ft / A = T * Fi / A = T * E
Exitance (Mr) = Reflectance (R) x Illuminance (E)
Exitance (Mt) = Transmittance (T) x Illuminance (E)
Other than glass and aluminum, building exterior and interior surfaces are diffusing reflective surfaces and not glossy or specular surfaces. By definition, a perfectly diffusing surface has constant luminous exitance for any angle of viewing.
Glare
Glare describes the discomfort level due to direct light in the field of vision. Glare is a relative term since it depends on the viewer. is the result of excessive, uncontrolled light within the field of view. The factors involved in producing discomfort glare are:
- The luminous intensity of the light source (candlepower, candelas)
- The size of each light source
- Position of each light source in the field of vision
- Adaptation level of the eye to the light source (depends on viewer)
- The background brightness
Adaptation level of the eye is a major factor. For example, when moving from a dark theatre to bright sunlight outside, the glare is intense. However, after some time the eye will adapt to the light and become comfortable with the intensity of the light source. This phenomenon is also called background brightness because the eye adapts to background brightness level.
Glare can be divided into
- Direct glare where the offending light source or brightness is in the field of view
- Reflected glare where the light "brightness" is reflected from the work surface
Direct glare can be controlled by keeping the luminous intensity values (brightness) of luminaries below maximum acceptable values. This can be done by breaking up the light source into smaller values and spreading it out.
Reflected glare from the work surface (that you are constantly looking at such as a book or desk) can be annoying and visually tiring. The tilt angle of the book or drafting table can be adjusted so the light from the light source is reflected away from the eye. Conversely, locate the light source behind over the shoulder of the viewer so that the light falling on the workplane is reflected away from the eye.
Glare measurements are based on a subjective (arbitrary) scale. The default value for glare in the DOE2 program for offices is 22. The maximum recommended glare value for art galleries is 16 and for rough work it is 28. The range is about 10 to 30.
Reflectance values of room surfaces can have an effect on the use of light in the room. For example you can defeat the purpose of indirect light luminaries, that depends on reflecting light from the ceiling, by using a dark ceiling.
For maximum lighting efficiency, the reflectances of room surfaces should be as high as possible, but not too high so as to create glare or a sterile looking environment. The recommended reflectance values are:
- Ceilings - 80% to 90%
- Walls - 40% to 60%
- Floors (tile) - 20% to 40% (carpeted floors have lower reflectances)
- Furniture - 20% to 45 %
The DOE2 program "defaults" for all surfaces is 0.5 (50%) and so reflectance values should be entered separately for each type of surface.
Note that reflectance values such as 0.9 (90%) apply to both specular reflection as in the case of mirrors and also to diffuse or scattered reflection as in the case of room interior surfaces.
Contrast
We need contrast to be able to see an object. A white object on a white background (example, white letters on white paper) is not distinguishable to the human eye. This is true of an object of any color against a background of the same color. A familiar use of contrast is word processing using computer monitors. The user can set the background and foreground colors that is most comfortable or to emphasize items.
Contrast can be measured as the ratio of foreground and background luminance levels. In the case of objects it is the ratio of task luminance against background luminance. In the case of reading material, it is the ratio of the luminance level of the letters (black has almost zero luminance) to the background paper (white has high luminance).
Contrast (C) is defined as the positive value of:
C = ( Lt - Lb ) / Lb C = ( Lb - Lt) / Lb C = ABS { ( Lb - Lt) / Lb } { 0 <= C <= 1 }
Lt and Lb are the luminance levels of the task area and the background area.
C = 0 for no contrast
C = 1 for maximum contrast
Since Luminance (L) is the product of Illuminance (E) and Reflectance (R), Contrast (C) can also be expressed as:
C = ( Rt - Rb ) / Rb C = ( Rb - Rt) / Rb C = ABS { ( Rb - Rt) / Rb } { 0 <= C <= 1 }
Rt and Rb are the Luminance Levels of the task area and the background area.
Example: A book on a desk is lighted to 100 footcandles (Illuminance = 100 lumens/sqft). The reflectance of the white page is 0.85 and that of the black print is 0.08.
M (white page) = 100 x 0.85 = 85 lumens/sqft
M (black print) = 100 x 0.08 = 8 lumens/sqft
The contrast (the difference in exitances) lets us see the black print.
Contrast refers to the difference in luminance between the target object and its background. Black letters on white paper have a high contrast compared to black letters on gray papers. A red object against a red background cannot be seen. Contrast (C) is calculated as the positive value of:
(Lt - Lb) / Lb where Lt = luminance of target (print) and Lb = luminance of background (paper)
The luminance values can be replaced with reflectances. In the example above the contrast is:
C = ( 0.08 - 0.85 ) / 0.85 = 0.9
Glare is bright light that interferes with vision.