Ductwork Design Program
Air Flow and Pressure Analysis
Preliminary Analysis
Information that is required to analyze a duct system for flow, pressures and sizes include:
- Supply or extract air quantities for each terminal device (diffuser, register, grille) in the room.
- The location of the terminal device in the room and the routing of ductwork from fan to terminal
- Design criteria limits for the project. These include:
Sizing method and associated velocity limits
Ductwork dimensional criteria
Static and total pressure limits to be used in
Fan Selection
Ductwork design and sizing
Air quantities for terminal devices located in each room can be calculated by the HVAC Application Loads Program. Locating terminal devices, assigning air quantities to them and during graphic input routing ductwork from the fans to the terminal devices.

Sizing Principles
Duct design is essentially a solution of two basic equations, the relationship between duct velocity, air quantity and duct cross-sectional area, Eq. 1, and Bernoulli's energy balance equation, Eq. 2.

| where: | 1,2 | = subscripts for stations 1 and 2 in the system |
| A | = cross-sectional area of duct (sq in.) | |
| V | = fluid average velocity (ft/min) | |
| Q | = airflow rate (cu ft/min) | |
| gc | = dimensional constant (lbm - ft)/(lbf - s2) | |
| P | = static pressure (lbf/sq ft) | |
| ρ | = fluid density (lbm/sq ft) | |
| ? | = ?g/gc = specific weight (lbf/cu ft) | |
| g | = acceleration due to gravity (ft/sec2) | |
| Z | = elevation (ft) | |
| P1 P2 | = gage pressures at stations 1 and 2 (lb/sq ft) | |
| PZ1 PZ2 | = atmospheric pressures at elevations Z1 and Z2 | |
| ΔPt | = total pressure loss between station 1 and station 2 in the system (lbf/sq ft) | |
| cf | = conversion factor (144) |
When the specific weight of atmospheric air γa is constant, it can be written that:
PZ1 - PZ2 = γa (Z2 - Z1)
Assuming that the specific weight of atmospheric air equals that of air within the duct, and combining Eq. 2 and 3 yields:

Head and Pressure
Head and pressure are often used interchangeably, but these terms have specific meanings.
Head is the height of a fluid column supported by fluid flow, while pressure is the normal force per unit area. With a liquid, it is convenient to measure the head of a fluid in terms of the flowing fluid. With a gas or air, however, it is customary to measure pressure on a column of liquid.
Static Pressure
Air exerts pressure on the walls of the duct in which it is confined. This pressure Ps is called static pressure at a station in the system and is positive or negative according to whether the pressure is greater or less than the ambient atmospheric pressure.
Velocity Pressure
The term (ρV2/2gc) in Eq. 2 is called the velocity pressure. Acting in the same direction as the flow of air, it is a measure of the kinetic energy. The velocity head (V2/2g) is independent of fluid density, while velocity pressure is not independent of density.

| where: | Pv | = velocity pressure (in. of water) |
| V | = fluid mean velocity (ft/min) | |
| ρ | = fluid density (lbm/cu ft) | |
| cf | = conversion factor (1097) |
Total Pressure
Total pressure is the sum of static pressure and velocity pressure:
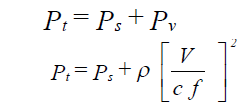
| where: | Pt | = total pressure (in. of water) |
| Ps | = static pressure (in. of water) | |
| Pv | = velocity pressure (in. of water) |
The pressure loss ΔPt in Eq. 2 is the resistance of a section of a duct system to flow and is composed of two elements:
- Duct friction, which as the name implies, is the frictional drag of the fluid moving along a rough surface, the duct wall.
- Dynamic loss, caused by restrictions and changes in direction to the flow through a piece of equipment (volume damper, heating coil, sound attenuator, etc.) and duct fittings.
Frictional Losses
When air flows through a duct, there is a loss of pressure due to the frictional drag of the air moving along the surfaces of the ducts.
For air flow in ducts, the friction loss may be calculated by the Darcy-Weisbach equation:

| where: | ρ | = fluid density (lbm/cu ft) |
| V | = fluid mean velocity (ft/min) | |
| ΔPfr | = friction losses in terms of total pressure (in. of water) | |
| fd | = friction factor, dimensionless | |
| L | = duct length (ft) | |
| D | = equivalent internal diameter of duct (in.) | |
| cf1 | = conversion factor (12) | |
| cf2 | = conversion factor (1097) |
Air flow in ducts follow two very different regimes: laminar flow at low velocities, and turbulent at high velocities. A transition zone in which flow may be either laminar or turbulent exists between the laminar and fully developed turbulent regions. Experimentation has determined two Reynolds numbers for which the flow is entirely laminar or turbulent. This dimensionless quantity, known as the Reynolds number Re, is defined by:

| where: | D | = equivalent internal diameter of duct (in.) |
| V | = fluid velocity in an equivalent round duct (ft/min) | |
| ρ | = fluid density (lbm/cu ft) | |
| μ | = fluid dynamic viscosity (lbm/ft x hr) | |
| cf | = conversion factor (5) |
Within the region of laminar flow (Reynolds numbers less than 2100). The friction factor fd is a function of the Reynolds number only, and it is ndependent of the roughness coefficient of the duct wall. It is defined by:

In completely turbulent regions (Reynolds numbers greater than 4000), the friction fd depends on the relative roughness of the duct material. It is independent of the Reynolds number and defined by:
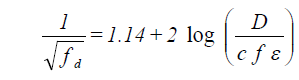
In the transition zone (Reynolds numbers between 2100 and 4000), the fraction fd depends on duct material absolute roughness and the Reynolds number represented by the Colebrook equation:

| where: | ε | = duct material absolute roughness (ft) |
| cf | = conversion factor, (12) |
If the air flow is smooth (Re < 2100), then Eq. 10 is used to determine the friction factor fd to solve the Darcy-Weisbach equation, Eq. 8, for friction drop through the duct section. To differentiate between transitional and rough turbulent flows, a value for fd is calculated from the equation for rough turbulent flows. Eq. 11. This is then used in Eq. 13 which is a close approximation of the curve which separates the rough flow from transitional on the Moody chart (ASHRAE Handbook: 1981 Fundamentals p. 4.10, fig. 13).
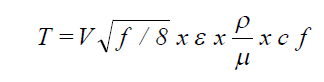
where: cf = conversion factor (2.16 x 10-6)
If T is greater than 100, the flow is rough and the value calculated for fd in Eq. 11 is representative of the flow. If T is less than 100, the flow is transitional and the value for fd obtained from Eq. 11 is used as a starting value to solve Eq. 12 iteratively for the friction factor for the flow. fd is then used in Eq. 8 to obtain the friction loss through the duct section.
Absolute Roughness
Duct material absolute roughness used by the program is shown in Fig. 1-6:
| Duct Material | Absolute Roughness, ? / ft |
| Uncoated Carbon Steel, Clean | 0.00015 |
| Aluminum | 0.0002 |
| Galvanized Steel, Hot Dipped | 0.0005 |
| Stainless Steel | 0.0003 |
| Fibrous Glass Duct, Rigid | 0.0003 |
| Flexible Duct, Metallic | 0.007 |
| Fibrous Glass Duct Liner | 0.015 |
Fig. 1-6: Duct Material Absolute Roughness
(reproduced with permission from ASHRAE Handbook: 1981 Fundamentals p. 33.5)
Frictional Losses for Noncircular Ducts
All friction loss calculations are based on the equivalent hydraulic diameter.
With equal length of round and rectangular ducts, constant flow in each duct, and equal resistance to flow in both the round and rectangular ducts, the equivalent round of a rectangular
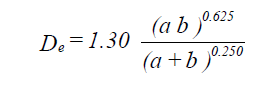
duct is:
| where: | De | = circular equivalent of a rectangular duct of equal length, fluid resistance and flow |
| a | = length of one side of duct (in.) | |
| b | = length of adjacent side of duct (in.) |
The mean velocity in a rectangular and oval duct will be less than its circular equivalent.
For oval ducts, the corresponding equations are:

| where: | P | = perimeter of oval duct (in. |
| a | = length of major axis (in.) | |
| b | = length of minor axis (in.) |
For both rectangular and oval ducts, the length of the sides is initially determined by the target aspect ratio. If the resulting dimensions fall outside the minimum and maximum allowable limits you have set, the dimensions are recalculated without using the target aspect ratio.
Dynamic Losses
Dynamic losses are caused by restrictions and changes in direction to the flow through a piece of equipment (volume damper, heating coil, etc.) and duct fittings. HVAC Systems Duct Design, SMACNA, 1985 lists the fittings available for round and rectangular ducts. Since little dynamic loss data for oval fittings are available, the data for rectangular fittings are used as an approximation.
Fittings
A duct fitting can occur anywhere along the length of a duct section. The program does not limit the number of fitting types or multiples thereof per duct section. If a fitting type is not available in the tables, its dynamic loss has to be entered as a special loss.
All the necessary engineering performance information for fittings is provided in the Ducts Program. The engineering design effort is to locate the appropriate fitting type in the duct network system. The duct fitting type and shape type should be compatible. Fittings are classified as junctions, transitions, and elbows.
| Junctions | Junctions are fittings which split the air stream into two or more branches. Converging junctions join two or more air streams into one and are basically used in a return/extract duct system. Fittings called take-offs, tees, and wyes are in this category. Loss coefficients for junctions are functions of the duct dimensions, air velocities and airflow rates. |
| Transitions | Transitions are fittings which change the duct size or shape without changing airflow direction or airflow rate. Transitions can be converging or diverging. Loss coefficients for transitions are functions of upstream and downstream duct velocities, angle of transition, transition length, and Reynolds number, Re. |
| Elbows | Elbows are fittings which change the direction of the air stream without changing the air quantity or velocity. The loss coefficients of elbows are functions of the elbow radius, duct dimensions, angle of turn, and Reynolds number, Re. |
By definition, a new duct section occurs when there is a change in air quantity, velocity, shape, duct material or duct insulation. Every duct section, therefore, begins with a junction or transition type fitting. These fittings are commonly referred to as take-off fittings. There is always one, and only one, take-off fitting per duct section.
Fitting Losses
Methods of computing the energy losses from the various fitting types are based on information found in ASHRAE Handbook: 1981 Fundamentals p. 33.28 through 33.50
The fluid resistance coefficient represents the ratio of the total pressure loss to the dynamic pressure at the referenced cross-section O:
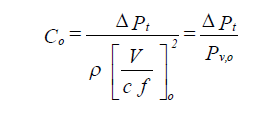
| where: | cf | = conversion factor (1097) |
| ΔPt | = total losses of fitting in terms of total pressure (in. of water) | |
| Co | = overall fluid resistance coefficient referenced to section O, dimensionless | |
| V | = average velocity to which coefficient Co is referenced (ft/min) | |
| Pv,o | = velocity pressure (in. of water) | |
| ρ | = fluid density (lbm/cu ft) |
For entries, exists, elbows and transitions, the fitting total pressure loss at section is calculated by:
ΔPt = Co Pv,o
where the subscript o is the cross section at which the velocity pressure is referenced.
For converging and diverging flow junctions, the total pressure loss through the main section is calculated as:
ΔPt = Cc,s Pv,c
For total pressure losses through the branch section
ΔPt = Cc,b Pv,c
| where: | Cc,s | = main local coefficient, dimensionless |
| Cc,b | = branch local coefficient, dimensionless | |
| Pv,c | = velocity pressure at the common section, c |
A tee nomenclature is shown in Fig. 1-7 for converging and diverging flow junction where,
ΔPt(s to c) = Cc,s Pv,c | ΔPt(c to s) = Cc,s Pv,c
ΔPt(b to c) = Cc,b Pv,c | ΔPt(c to b) = Cc,b Pv,c
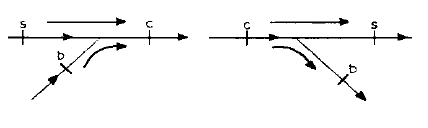
(reproduced with permission from ASHRAE Handbook:
1981 Fundamentals, Fig. 6, p. 33.8)
Fan Pressures, Mechanical Energy
For a supply duct system, a circuit is defined as the succeeding sections of ductwork from the fan discharge up to either a terminal device or a primary damper (for constant-volume, fan-powered boxes only). For an extract duct system, a circuit is defined as the succeeding section of ductwork from a terminal device up to a fan.
The number of circuits in a duct system is, by definition, equal to the number terminal devices and/or constant-volume, fan-powered boxes.
The supply and extract duct systems are run independently; however, the supply system does need the total pressure losses from the extract system in order to determine the fan total pressure if a return fan is not specified. Therefore, the extract duct system should be run first, the total pressure losses of the extract duct system are compared to the loss from the outdoor intake to the mixing box. The greater of the two is used as miscellaneous duct losses for the supply system.

The total pressure losses for each section of a duct system are calculated by Eq. 22:
| where: | ΔPt | = total pressure loss for section of ductwork (in. of water) |
| ΔPi | = fitting total pressure loss (in. of water) | |
| n | = number of fittings within a section of ductwork | |
| ΔPj | = equipment (damper, coil, etc.) total pressure loss (in. of water) | |
| m | = number of pieces of equipment within a section of ductwork | |
| ΔPk | = duct friction loss in terms of total pressure (in. of water) |
The total pressure drop through each circuit is calculated by summing the pressure loss through each section in the circuit.
The fan total pressure requirement for an extract duct system is given by the expressions:
Pt = ΔPt + SEFi + SEFo + ΔPf + ΔPd
| where: | Pt | = fan total pressure (in. of water) |
| ΔPt | = pressure drop through critical circuit, circuit with maximum resistance to flow ("H2O) | |
| SEFi | = system effect factor due to fan inlet conditions (in. of water) | |
| SEFo | = system effect factor due to fan outlet conditions (in. of water) | |
| ΔPf | = total pressure loss through fan components such as coils, filters, etc. ("H2O) | |
| ΔPd | = total pressure loss through miscellaneous ductwork such as ductwork downstream of the fan for an extract system, or extract or return ductwork for a supply system ("H2O) |
Duct Sizing
The sections of supply duct systems can be sized using one of the following methods:
- Pre-sized
- equal friction
- static regain
- total pressure
- velocity reduction
- constant velocity
Equal friction and constant velocity are the only methods for the design of extract duct systems.
For a draw-through fan, the first section is the one immediately downstream of the fan outlet. If the supply fan arrangement is blow-through, the first section of the ductwork is the section immediately downstream of the cooling coil. If the fan has a discharge plenum, the first section of the ductwork is the one immediately following the plenum. You should identify the first section and lay out the duct network accordingly.
The static regain, total pressure and velocity reduction sizing methods cannot be used to size duct sections downstream of terminal boxes. If you select one of these three methods downstream of a terminal box, the program will automatically default to the equal friction method.
Flexible ducts are always considered round in shape. They are sized using the velocity you specify.
Pre-Sized Method
The pre-sized method can be used to calculate pressure losses for a system with pre-calculated duct dimensions. If you choose this method, the program will check the network for duct dimensions. Only if all sections are sized will it calculate pressure drops through each section and determine critical circuits.
Equal Friction Sizing Method
In the equal friction method, the system is sized for a constant pressure loss per unit length of duct. The equal friction method can be used for the design of supply and extract duct systems.
The program offers two options for this method. The first option, called ASHRAE Limits, allows the designer to specify high and low limits for pressure loss per unit length and velocity.
For the other option, you can specify the pressure loss per unit length and the maximum and minimum velocity for the sections of a duct system.
The equal friction sizing method works iteratively between the minimum and maximum velocity limits to determine a duct size that results in the specified pressure loss per unit length. You can also request a pressure analysis of the network.
Static Regain Sizing Method
For this method, a section of the duct system is sized so that the increase in static pressure due to velocity reduction from its upstream section, offsets the friction loss in the section. As in the other sizing methods, the program starts sizing with the first section. If you have not specified any overrides for the ducts in that section, it is sized based on the maximum velocity you specified.
When sizing any other section, the program searches upstream of that section until it finds a section that also used the static regain sizing method. The velocity at the exit of that section is used as the upper velocity limit for the section to be sized; the minimum you specified is used as the lower limit. The program searches iteratively between these limits to calculate a duct size that results in the required static regain. If the static regain calculated is less than that required even at minimum velocity, the section is sized using minimum velocity.
If the program encounters a section where all upstream sections are pre-sized, that section is sized using maximum velocity and the sizing method is applicable starting at that section.
Essentially, the program disregards any sections that have been overridden or that use another sizing method.
The advantage of this method is that all sections have approximately the same entering static pressure, thereby simplifying outlet selection. One disadvantage might be seen in networks with a large pressure drop in a section near the fan outlet. The velocity could be reduced to the minimum within a few sections in such a way that all the ductwork downstream would be sized using minimum velocity. Another disadvantage could stem from specifying a very low minimum velocity. Ducts would then tend to be very large at the end of long branch runs. The sizing method does not account for the total mechanical energy supplied to the air by the fan.
Total Pressure Sizing Method
The total pressure sizing method is a variation of the static regain method. The total pressure of any point in the ductwork represents the actual energy of the moving air at that point.
The program will search for the first section that does not have override dimensions. This section is sized at the maximum velocity you have specified. When sizing any other section, the program searches upstream until it finds a section that also used the total pressure sizing method. The total pressure leaving that section is considered equal to the total pressure entering the section to be sized. The program then uses binary convergence, starting with the minimum velocity, until it finds a duct size that matches the required entering total pressure. All presized duct sections are disregarded when applying the total pressure sizing method to the sections to be sized.
The advantage of this method is that it accounts for all mechanical energy losses in a system. The system design does not have to be dependent on an assumed velocity at the fan outlet.
Velocity Reduction Sizing Method
This method sizes the first section for the maximum velocity that you specified and designs the downstream sections at progressively lower velocities using the reduction percentage you also specified. The velocity cannot fall below the minimum that you specified.
If the section immediately above the section to be sized is a presized section, the program searches upstream until it finds a section that also used the velocity reduction sizing method and treats it as the upstream section for the section to be sized.
Constant Velocity Sizing Method
The constant velocity method is a design in which every section of a duct system is sized based on the design velocity you specified. This design velocity may be overridden for any section of the system. Maximum and minimum velocity limits are not applicable in this method. Flexible ducts are also sized based on a design velocity you specified. The constant velocity method can be used for the design of supply and extract duct systems.
Circuit Analysis and System Balancing
The series of duct sections starting from the primary fan/air handling unit section to the duct section with an opening is defined as a circuit. The number of duct circuits in a duct system is, by definition, equal to the number of supply and exhaust openings (registers, grilles or diffusers).
Circuit pressure analysis consists of the following steps:
- Add the pressure losses in each section of the circuit to obtain the circuit pressure loss.
- Determine the highest circuit pressure loss.
- Set the entering total pressure of the first section in the circuit as the sum of the highest circuit pressure loss and the velocity pressure in the section.
- Analyze each section in the circuit starting with the first section and moving through each section in the fluid flow sequence.
The entering section total pressure is the leaving section total pressure of the upstream section.
The leaving section total pressure is the entering section total pressure less the section pressure loss.
The entering and leaving section static pressures are obtained by deducting the velocity pressure at these nodes. - Calculate the balancing required in each circuit. This is equal to the highest circuit total pressure loss minus the given circuit total pressure loss.
In the case of primary-secondary systems, the primary circuit ends at the fan-powered box or the terminal device if there is no box in the circuit.
Secondary systems are analyzed independently as separate systems. The entering pressure of the first section in the secondary system is the pressure loss of the secondary circuit with the highest pressure loss.
The objective of system balancing is to maintain the same pressure loss in all circuits. Dampers at the end of each circuit will still be required, but are used to make the fine tuning adjustment to maintain the right air quantity at each opening.
Using the specified sizing method, the Ducts Program makes the preliminary analysis and calculates sizes for all sections of the duct system. It next determines the circuit with the highest pressure loss. This circuit is commonly referred as the longest hydraulic run. All other circuits will have to be dampered. The amount of dampering is directly related to the difference between the pressure loss of the given circuit and the highest pressure loss of the system.
The system balancing process involves a series of iterations to increase the pressure losses of all circuits to that of the circuit with the highest pressure loss. The process starts with the circuit with the next highest pressure loss and continues in descending order of circuit pressure loss. Duct sections in the circuit and that are not common to the previously analyzed circuits are iteratively reduced in size until the circuit pressure loss is equal to the loss in the longest run. There are limits to the process of reducing sizes. The iteration stops when the pressure loss, velocity and noise levels in the duct section reaches the maximum limits of the design criteria. In this case, the circuit still remains unbalanced and requires dampering. Output reports indicate the amount of dampering required by each circuit.
Thermal Analysis
After the duct network has been sized, the system can be analyzed to calculate heat gains or losses in the network.
The thermal analysis option is available only for systems that satisfy the following criteria:
- There are no terminal boxes in the network with reheat coils.
- All rooms are in either the heating or cooling mode.
- There are no secondary heating coils in the system.
The program begins the thermal analysis with the first section in the ductwork. The temperature of air entering the first section is the same as the coil leaving temperature for a blow-through system. For a draw-through system, the temperature of air entering the first section is adjusted for heat gain across the fan. For a motor that is inside the airstream, the heat gain is given by
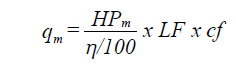
For a motor that is outside the airstream, the heat gain is
qb = HPm x LF x cf
| where: | qm | = heat gain from electric motor (Btu/hr) |
| HPm | = horsepower rating for the motor | |
| η | = full load motor efficiency (%) | |
| LF | = load factor, i.e. a fraction of rated load delivered | |
| cf | = conversion factor (745.7) |
The horsepower rating and full load efficiency are obtained from Fig. 1-8.
The temperature rise across the fan is then calculated using the following equation:
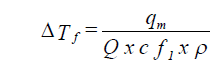
| where: | ΔTf | = temperature rise across the fan (oF) |
| qm | = heat gain from electric motor (Btu/hr) | |
| Q | = air flow quantity (cu ft/min) | |
| cf1 | = conversion factor (14.4) | |
| ρ | = air density (lbm/cu ft) |
| Rated Motor HP | Full Load Efficiency % | Rated Motor HP | Full Load Efficiency % |
| 0.16 | 35 | 20 | 87 |
| 0.25 | 54 | 25 | 88 |
| 0.33 | 56 | 30 | 89 |
| 0.50 | 60 | 40 | 89 |
| 0.75 | 72 | 50 | 89 |
| 1 | 77 | 60 | 89 |
| 2 | 79 | 75 | 90 |
| 3 | 81 | 100 | 90 |
| 5 | 82 | 125 | 90 |
| 7.5 | 84 | 150 | 91 |
| 10 | 85 | 200 | 91 |
| 15 | 86 | 250 | 91 |
Fig. 1-8: Heat Gains from Typical Electric Motors
(reproduced with permission from ASHRAE Handbook: 1981 Fundamentals p. 26.26, Table 24)
Once the temperature of air entering the first section is determined, the individual sections can be analyzed for heat gains or losses. The program calculates heat gains or losses using the following expressions:


| where: | Y | = cf1 AV?/UPL for rectangular and oval ducts |
| y | = cf2 DV?/UL for round ducts | |
| qe | = heat loss/gain through duct walls (Btu/hr) (Negative for heat gain) | |
| U | = overall coefficient of heat transfer of duct walls (Btu/sq ft. oF) | |
| P | = perimeter of duct (in.) | |
| A | = cross-sectional area of duct (sq in.) | |
| D | = duct diameter (in.) | |
| L | = duct length (ft) | |
| ρ | = density (lbm/cu ft) | |
| and: | ||
| te | = temperature of air entering duct (oF) | |
| ti | = temperature of air leaving duct (oF) | |
| ta | = temperature of air surrounding duct, (oF) | |
| cf | = conversion factor (2.4) | |
| cf1 | = conversion factor (2.4) | |
| cf2 | = conversion factor (0.6) |
The U-values used in the program for sheet metal, lined and insulated ducts are shown in Fig 1-9.
(reproduced with permission from ASHRAE Handbook: 1981 Fundamentals, p. 33.10, Fig. 8)
Reanalysis Options
The program provides two ways to reanalyze heat gains and losses. You can choose to
- Recalculate air flow quantities at each terminal device
- Adjust the coil leaving temperature
Option One
The first option is to recalculate air flow quantities required at each terminal device in order to satisfy the design cooling or heating loads in each room. This is done by comparing the actual supply air temperature to the design supply air temperature that you can specify for each room. The following expression is used to recalculate the air flow quantities:
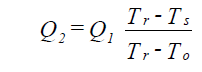
| where: | Q1 | = design supply air quantity (cu ft/min) |
| Q2 | = recalculated supply air quantity (cu ft/min) | |
| Tr | = design room dry-bulb temperature (oF) | |
| Ts | = design supply air temperature at terminal device (oF) | |
| To | = actual supply air temperature at terminal device (oF) |
Once the supply air quantities are adjusted, the program then resizes the ductwork and has the option of performing pressure, acoustic and thermal analyses for the new network.
Option Two
The second option is to recalculate the coil leaving temperature by an amount equal to the temperature difference in the circuit with the maximum temperature rise or drop.
For a network that has net heat gain across the sections, the coil leaving temperature is lowered so that the design supply air temperature can be maintained at the terminal device for the circuit with the maximum temperature rise. For a network that has net heat loss across the sections, the coil leaving temperature is increased so that design supply air temperature can be maintained at the terminal device for the circuit with the maximum temperature drop.
The next step is to recalculate supply air quantities for all other terminal devices in order to satisfy design cooling or heating loads for each room.
Once the required air quantities are recalculated, the program then resizes the network and has the option of performing pressure, acoustic and thermal analyses for the network.
Acoustic Analysis and System Noise Attenuation
The program determines the amount of required attenuation on the inlet and discharge sides of the fan(s), or in the main ductwork and branches as described below.
For each circuit, the program determines the resultant attenuation provided by the following items:
- In straight, line and unlined duct
- In lined and unlined elbows
- Fan discharge plenum (supply ductwork only)
- Branch takeoffs
- Duct and reflection loss
- Room effect
The resultant sound power level per terminal device (inlet or outlet) is the difference between the attenuation of the ductwork system and room effect (items 1 through 6) and the fangenerated sound power level for all eight octave bands. The difference between this resultant sound power level per diffuser and the sound pressure levels that correspond with the specified room criterion (NC level) represents the attenuation required on the inlet and discharge sides of the fan(s), or in the main ductwork and branches.
Fig. 1-10 summarizes the system noise procedure described for each circuit.
| Line | Item |
| 1 | Fan Lq re 10-2 watts |
| 2 | Attenuation of duct system |
| 3 | Branch take-offs and room effect attenuation |
| 4 | Total system attenuation, line 2 + line 3 |
| 5 | Sound Power level per terminal device |
| 6 | Room criterion (NC level), line 1 - line 4 |
| 7 | Required attenuation, line 5 - line 6 |
Fig. 1-10: Summary Table
On determining the resultant sound power level for each circuit, the program does not take into account the following items:
- attenuation through terminal boxes
- terminal box discharge sound power level
- regenerated noise at fitting
- attenuation in fittings other than elbows and branch takeoffs
Fan Noise
The sound power generation of a given fan obtained from the fan manufacturer may be entered using the fan sound power levels input form. However, if the data are not available, the program can estimate the octave band sound power levels for various fans using the following expression:
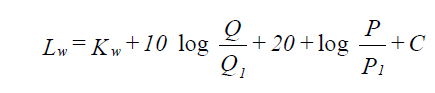
| where: | Lw | = estimated sound power level of fan (dB re 1pW) |
| Kw | = specific sound power level from table | |
| Q | = flow rate (cu ft/min) | |
| Q1 | = 1 when flow is in sq ft/min | |
| P | = Fan static pressure (in. of water) | |
| P1 | = 1 when pressure is in in. of water | |
| C | = correction factor in dB, for point of operation |
The values of the estimated sound power level Lw are calculated for all eight bands using Eq. 30, and the BFI (see Fig. 1-11) is added to the octave band in which the blade passage frequency falls. Fig. 1-12 is used to determine the octave band in which blade frequency increment (BFI) occurs for the various types of fans.
| Fan Type | Fan Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | BFI | ||
| Centrifugal Airfoil backward curved, | >= 36 in. | 32 | 32 | 31 | 29 | 28 | 23 | 15 | 10 | 3 |
| Backward inclined | < 36 in. | 36 | 38 | 36 | 34 | 33 | 38 | 20 | 15 | |
| Forward, curved | All | 47 | 43 | 39 | 33 | 28 | 25 | 23 | 20 | 2 |
| Radial blade, | > 40 in. | 45 | 39 | 42 | 39 | 37 | 32 | 30 | 29 | |
| Pressure blower | 40 in.-20 in. 20 in. | 55 63 | 48 57 | 48 58 | 45 50 | 45 44 | 40 39 | 38 38 | 36 37 | 8 |
| Vaneaxial | >= 40 in. 40 in. | 39 37 | 36 39 | 38 43 | 39 43 | 37 43 | 34 41 | 32 38 | 30 35 | 6 |
| Tubeaxial | >= 40 in. 40 in. | 41 40 | 39 41 | 43 47 | 41 46 | 39 44 | 37 43 | 34 37 | 31 32 | 5 |
| Propeller Cooling tower | All | 48 | 51 | 58 | 55 | 52 | 46 | 40 | 5 | |
Fig. 1-11: Sound Power Levels
Specific sound power levels for inlets or outlets.
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.7, p. 11.14)
| Fan Type | Octave Band |
| Centrifugal Airfoil, backward curved, backward inclined Forward curved Radial blade, pressure blower | 250 Hz 500 Hz 125 Hz |
| Vaneaxial | 125 Hz |
| Tubeaxial | 63 Hz |
| Cooling Tower Propeller | 63 Hz |
Fig. 1-12: Octave Band
Octave band in which blade frequency increment occurs.
(reproduced with permission from 1987 ASHRAE Handbook, Table 4, p. 52.7)
Point of Operation
The specific sound power levels given in Fig. 1-11 are for fans operating at or near the peak efficiency point of the fan performance curve. If a fan is not operating at or above 90% of peak static efficiency, a correction factor, C (see Eq. 30), is added to the specific sound power levels given in Fig. 1-13 for all eight octave bands. Fig. 1-12 gives the correction factor C as a function of percent of peak static efficiency.
| Static Efficiency % of Peak | Correction Factor dB |
| 90 to 100 | 0 |
| 85 to 89 | 3 |
| 75 to 84 | 6 |
| 65 to 74 | 9 |
| 55 to 64 | 12 |
| 50 to 54 | 15 |
Fig. 1-13: Correction Factor C
Correction factor, C, for off-peak operation (reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.8, p. 11.15)
Fans In Parallel
The program can accept up to ten fans in parallel. These fans must be of the same type and produce the same static pressure and flow rate. The resultant sound power levels of two or more fans in parallels for all octave bands are obtained from Fig. 1-14.
| Difference between sound levels in dB | No. of dB to be added to higher level |
| 0 | 3.0 |
| 1 | 2.6 |
| 2 | 2.1 |
| 3 | 1.8 |
| 4 | 1.5 |
| 5 | 1.2 |
| 6 | 1.0 |
| 7 | 0.8 |
| 8 | 0.6 |
| 10 | 0.4 |
| 12 | 0.3 |
| 14 | 0.2 |
Fig. 1-14: Combining Decibels
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.1, p. 11.2)
| Example: | Find the resultant sound power levels of three fans in parallel having an estimated sound power level equal to 90 dB at the 125 octave band using Fig. 1-14. |
Solution:
- 90 dB - 90 dB = 0 dB from Fig. 1-14, 3 dB is added to the higher level 90 dB. The resultant sound power level for 2 fans in parallel is 90 + 3 = 93 dB.
- 93 dB - 90 dB = 3 dB from Fig. 1-14, 1.8 dB is added to the higher level 93 dB. The resultant sound power level for 3 fans in parallel is 93 + 1.8 = 94.8 dB.
Fan Discharge Air Plenum
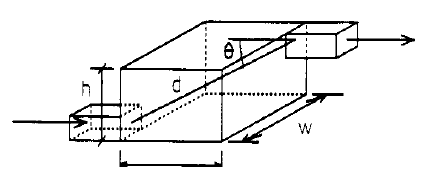
The sound attenuation provided by a plenum on the fan discharge shown in Fig. 1-15 is

| where: | α | = absorption coefficient of lining, dimensionless |
| Se | = plenum exit area (sq ft) | |
| Sw | = plenum wall area (sq ft) | |
| dr | = distance between entrance and exit (ft) | |
| θ | = angle of incident at exit, degrees |
Attenuation of the Duct System
The program calculates the natural attenuation of unlined rectangular and round duct sections of the duct system using Fig. 1-16 and Fig. 1-17. These tables give the natural attenuation for linear length as a function of the duct dimension for all the eight octave bands.
Fig. 1-16 is also used for oval ducts. The program uses the smallest duct dimensions for rectangular and oval ducts. The attenuation values given in Fig. 1-16 and Fig. 1-17 are doubled if the unlined duct section has an external insulation.
The program calculates the natural attenuation of lined rectangular and round duct sections and elbows using Fig. 1-18 through Fig. 1-21. These tables give the attenuation as a function of duct dimension and lining thickness for all eight octave bands.
Fig. 1-18 and Fig. 1-19 are also used for oval ducts. The program uses the smallest duct dimension for rectangular and oval ducts. The attenuation values given in Fig. 1-18 through Fig. 1-21 are used for duct sections of only a maximum of 15 linear feet of lined duct, lined duct sections of over 15 linear feet are considered as unlined duct.
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Rectangular Duct dB/ft | 3"-12" | .10 | .10 | .05 | .05 | .04 | .04 | .04 | .04 | |
| 13"-18" | .15 | .10 | .05 | .05 | .04 | 04 | 04 | 04 | ||
| 19"-24" | .18 | .12 | .06 | .05 | .04 | 0.4 | 0.4 | 0.4 | ||
| 25"-36" | .20 | .14 | .06 | .05 | .04 | 0.4 | 0.4 | 0.4 | ||
| 37"-48" | .20 | .14 | .06 | .05 | .04 | .04 | .04 | .04 | ||
| 49"-72" | .20 | .15 | .06 | .05 | .04 | .04 | .04 | .04 | ||
| 73"-96"+ | .20 | .16 | .07 | .05 | .04 | 0.4 | 0.4 | 0.4 | ||
Fig. 1-16: Attenuation, Unlined Rectangular and Oval Ducts
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10A, p. 11.16)
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Round Duct dB/ft | 3"-5" | .03 | .03 | .02 | .02 | .01 | .01 | .01 | .01 | |
| 6"-12" | .03 | .03 | .02 | .02 | .01 | .01 | .01 | .01 | ||
| 13"-18" | .02 | .02 | .01 | .01 | 0 | 0 | 0 | 0 | ||
| 19"-24" | .02 | .02 | .01 | .01 | 0 | 0 | 0 | 0 | ||
| 25"-36" | .02 | .02 | .01 | .01 | 0 | 0 | 0 | 0 | ||
| 37"-48" | .01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 49"-72" | .01 | .01 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 73"-96"+ | .01 | .01 | 0 | 0 | 0 | 0 | 0 | 0 | ||
Fig. 1-17: Attenuation, Unlined Round Ducts
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10B, p. 11.16)
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Rectangular Duct dB/ft 1" lining | 3"-5" | .3 | .6 | 1.0 | 2.1 | 5.0 | 10.5 | 5.0 | 4.0 | |
| 6"-12" | .2 | .4 | .9 | 1.9 | 4.3 | 7.5 | 2.0 | 2.0 | ||
| 13"-18" | .2 | .3 | .6 | 1.5 | 3.7 | 3.0 | 1.0 | 1.0 | ||
| 19"-24" | .2 | .2 | .5 | 1.4 | 3.5 | 1.8 | .8 | .8 | ||
| 25"-36" | .2 | .2 | .4 | 1.0 | 1.8 | 1.2 | .6 | .6 | ||
| 37"-48" | .2 | .2 | .3 | .9 | 1.5 | 1.0 | .4 | .4 | ||
| 49"-72" | .2 | .2 | .25 | .8 | 1.0 | .8 | .3 | .3 | ||
| 73"-96"+ | .2 | .2 | .25 | .7 | .8 | .7 | .2 | .2 | ||
Fig. 1-18: Rectangular Duct, 1 Inch Lining
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10E, p. 11.17)
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Rectangular Duct dB/ft with 1/2" lining | 3"-5" | .2 | .4 | .7 | 1.3 | 2.5 | 5.0 | 5.0 | 4.0 | |
| 6"-12" | .2 | .3 | .6 | 1.1 | 2.2 | 4.5 | 2.0 | 2.0 | ||
| 13"-18" | .2 | .25 | .5 | 1.0 | 2.0 | 1.5 | 1.0 | 1.0 | ||
| 19"-24" | .2 | .2 | .4 | .8 | 1.6 | 1.4 | .8 | .8 | ||
| 25"-36" | .2 | .2 | .3 | .6 | 1.2 | 1.0 | .6 | .6 | ||
| 37"-48" | .2 | .2 | .2 | .4 | .8 | .8 | .3 | .3 | ||
| 49"-72" | .2 | .2 | .2 | .3 | .5 | .5 | .3 | .3 | ||
| 73"-96"+ | .2 | .2 | .2 | .2 | .4 | .2 | .2 | .2 | ||
Fig. 1-19: Rectangular Duct, 1/2 Inch Lining
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10F, p. 11.17)
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Round Duct dB/ft with 1" lining | 6"-12" | .3 | 1.0 | 1.5 | 1.5 | 3.7 | 4.8 | 2.8 | 2.2 | |
| 13"-18" | .2 | .7 | 1.0 | 1.2 | 2.7 | 2.8 | 1.5 | 1.3 | ||
| 19"-24" | .1 | .5 | .6 | 1.0 | 1.7 | .9 | .5 | .5 | ||
| 25"-36" | .07 | .2 | .4 | .8 | 1.0 | .7 | .5 | .5 | ||
| 37"-48" | .04 | .08 | .3 | .6 | .6 | .5 | .5 | .5 | ||
| 49"-72" | .02 | .02 | .2 | .5 | .5 | .4 | .4 | .4 | ||
| 73"-96"+ | .01 | .02 | .1 | .4 | .4 | .3 | .3 | .3 | ||
Fig. 1-20: Round Duct, 1 Inch Lining
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10G, p. 11.17)
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Round Duct dB/ft with 2" lining | 6"-12" | .5 | 1.2 | 1.7 | 2.3 | 3.9 | 5.0 | 3.0 | 2.3 | |
| 13"-18" | .4 | 1.0 | 1.2 | 2.2 | 3.0 | 3.0 | 1.7 | 1.5 | ||
| 19"-24" | .3 | .8 | .9 | 2.1 | 2.0 | 1.0 | .8 | .7 | ||
| 25"-36" | .2 | .3 | .7 | 1.5 | 1.5 | .8 | .6 | .6 | ||
| 37"-48" | .12 | .2 | .5 | 1.0 | 1.0 | .7 | .6 | .6 | ||
| 49"-72" | .08 | .1 | .3 | .7 | .7 | .5 | .5 | .5 | ||
| 73"-96"+ | .06 | .08 | .2 | .6 | .6 | .4 | .4 | .4 | ||
Fig. 1-21: Round Duct, 2 Inch Lining
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10H, p. 11.17)
The attenuation of unlined rectangular and round elbows is given in Fig. 1-22. The program doubles the attenuation values given in this table if the unlined elbow has external insulation.
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of Unlined Elbows Rectangular Duct dB/ft | To 4" | 0 | 0 | 0 | 0 | 0 | 1.0 | 2.0 | 3.0 | |
| 5"-10" | 0 | 0 | 0 | 0 | 1.0 | 2.0 | 3.0 | 3.0 | ||
| 11"-20" | 0 | 0 | 0 | 1.0 | 2.0 | 2.0 | 3.0 | 3.0 | ||
| 21"-40" | 0 | 0 | 1.0 | 2.0 | 3.0 | 3.0 | 3.0 | 3.0 | ||
| 41"-80"+ | 0 | 1.0 | 2.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | ||
Fig. 1-16: Unlined Rectangular and Round Elbows
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10C, p. 11.16)
The attenuation of lined rectangular and round elbows is given in Fig. 1-23.
| Smallest Duct Dimension | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Attenuation Of lined Elbows Round & Rectangular Duct dB/ft | To 4" | 0 | 0 | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | |
| 5"-10" | 0 | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 8.0 | ||
| 11"-20" | 0 | 1.0 | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 | |||
| 21"-40" | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 8.0 | 10.0 | ||
| 41"-80"+ | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 8.0 | 10.0 | 12.0 | ||
Fig. 1-23: Lined Rectangular and Round Elbows
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10D, p. 11.16)
| Octave Band Center Frequency Hz | ||||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Branch Duct Attenuation | 0.2% | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | |
| 0.5% | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | ||
| 1.0% | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | ||
| 2.0% | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | ||
| 5.0% | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | ||
| 10.0% | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | ||
| 20.0% | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | ||
| 50.0% | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||

Fig. 1-24: Branch Takeoff Attenuation
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.11A, p. 11.18)
The program calculates the attention of branch takeoffs using Fig. 1-24. This table gives the branch duct attenuation as a function of the percentage of the room to the system air flow quantities for all eight octave bands.
The program computes the attenuation available through end reflection loss using Fig. 1-25.
| Smallest Duct Dimensions | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| Duct Diameter End Reflection Loss | To 5" | 17 | 12 | 8 | 4 | 1 | 0 | 0 | 0 | |
| 6"-8" | 14 | 10 | 6 | 2 | 0 | 0 | 0 | 0 | ||
| 9"-12" | 12 | 8 | 4 | 1 | 0 | 0 | 0 | 0 | ||
| 13"-16" | 10 | 6 | 2 | 0 | 0 | 0 | 0 | 0 | ||
| 17"-22" | 8 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| 23"-30" | 6 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 31"-40" | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 41"-60"+ | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
Fig. 1-25: Duct End Reflection Loss
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10B, p. 11.18)
| Room Volume | Ceiling Height | Octave Band Center Frequency Hz | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | ||||
| Room Effect (for average rooms) | 1000 | 8' | 2 | 2 | 2 | 2 | |||||
| 2000 | 8' | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | ||
| 5000 | 8'-12" | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | ||
| 10000 | 8'-10" | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 10 | ||
| 10000 | 11'-14" | 8 | 9 | 9 | 9 | 10 | 10 | 10 | 11 | ||
| 20000 | 8'-12" | 8 | 9 | 9 | 10 | 10 | 11 | 11 | 12 | ||
| 20000 | 13'-15" | 9 | 10 | 10 | 11 | 11 | 12 | 12 | 13 | ||
| 30000 | 8'-11" | 11 | 12 | 12 | 12 | 13 | 13 | 13 | 14 | ||
| 30000 | 12'-15" | 12 | 13 | 13 | 13 | 14 | 14 | 14 | 15 | ||
| 40000+ | 8'-14" | 10 | 11 | 11 | 12 | 12 | 13 | 13 | 14 | ||
| 40000+ | 15'-17" | 11 | 12 | 12 | 13 | 13 | 14 | 14 | 15 | ||
| 40000+ | 18'-22" | 12 | 13 | 13 | 14 | 14 | 15 | 15 | 16 | ||
Fig. 1-26: Room Effect Attenuation
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.10C, p. 11.18) The program calculates the room effect attenuation using Fig. 1-26. This table gives the attenuation for room with suspended ceilings as a function of the ceiling height and room volume for all eight octave bands.
Room Criteria
Fig. 1-27 gives the sound pressure levels for all eight octave bands that correspond with a specified NC level for the room.
| Octave Band Center Frequency Hz | ||||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |||
| NC Noise Criterion Levels | NC-30 | 57 | 48 | 35 | 31 | 29 | 28 | 28 | 27 | |
| NC-35 | 60 | 53 | 46 | 40 | 36 | 34 | 33 | 32 | ||
| NC-40 | 64 | 57 | 51 | 45 | 41 | 39 | 38 | 37 | ||
| NC-45 | 67 | 60 | 54 | 49 | 46 | 44 | 43 | 42 | ||
| NC-50 | 71 | 64 | 59 | 54 | 54 | 49 | 48 | 47 | ||
Fig. 1-27: Sound Pressure Levels
(reproduced with permission from HVAC Systems Duct Design, SMACNA, Table 11.11D, p. 11.18)
Material Estimation
Classification of Ducts
This feature of the program allows you to select a gage or thickness and reinforcement required for the ducts once they have been sized.
Operating pressures for each section of ductwork are calculated earlier during the pressure analysis. Fig. 1-28 gives the pressure class for each section and corresponding operating pressure. Once the operating pressures are determined, the sections are analyzed based on the specified shape, rectangular/oval or round.
| Static Pressure | |
| Pressure Class | Operating Pressure |
| 0.5 in. of water | up to 0.5 in. of water |
| 1 in. of water | over 0.5 in. of water to 1 in. of water |
| 2 in. of water | over 1 in. of water to 2 in. of water |
| 3 in. of water | over 2 in. of water to 3 in. of water |
| 4 in. of water | over 3 in. of water to 4 in. of water |
| 6 in. of water | over 4 in. of water to 6 in. of water |
| 10 in. of water | over 6 in. of water to 10 in. of water |
Fig. 1-28 Operating Pressures
(reproduced with permission from HVAC Duct Construction Standards, SMACNA, p. 106)
Duct Materials
The thickness and weight of sheet-metal sheets available in the program are given in Fig. 1-29 through Fig. 1-32 reproduced with permission from HVAC Duct Construction Standards, SMACNA, Appendix 1 through 4. The program uses the nominal thicknesses from the tables. Minimum and maximum thicknesses are shown for your information only.
| Gage | Thickness in Inches | Weight Lb/ft2 | ||
| Min | Max | Nom | ||
| 30 | .0105 | .0145 | .0125 | .525 |
| 28 | .0136 | .0176 | .0156 | .656 |
| 27 | .0142 | .0202 | .0172 | .722 |
| 26 | .0158 | .0218 | .0188 | .788 |
| 25 | .0189 | .0249 | .0219 | .919 |
| 24 | .0220 | .0280 | .0250 | 1.050 |
| 23 | .0241 | .0321 | .0281 | 1.181 |
| 22 | .0273 | .0353 | .0313 | 1.313 |
| 21 | .0304 | .0384 | .0344 | 1.444 |
| 20 | .0335 | .0415 | .0375 | 1.575 |
| 19 | .0388 | .0488 | .0438 | 1.838 |
| 18 | .0450 | .0550 | .0500 | 2.100 |
| 17 | .0513 | .0613 | .0563 | 2.363 |
| 16 | .0565 | .0685 | .0625 | 2.625 |
| 15 | .0643 | .0763 | .0703 | 2.953 |
| 14 | .0711 | .0851 | .0781 | 3.281 |
| 12 | .0100 | .1184 | .1094 | 4.594 |
| 11 | .1150 | .1350 | .1250 | 5.250 |
Fig. 1-29: Stainless Steel
(reproduced with permission from HVAC Duct Construction Standards, SMACNA, Appendix 1)
| M.S. Gage | Weight lb/ft2 | Thickness | ||
| Nominal | Cold Rolled | |||
| Min | Max | |||
| 28 | .625 | .0149 in | .0129 in | .0169 in |
| 26 | .750 | .0179 in | .0159 in | .0199 in |
| 24 | 1.000 | .0239 in | .0209 in | .0269 in |
| 22 | 1.250 | .0299 in | .0269 in | .0329 in |
| 20 | 1.500 | .0359 in | .0329 in | .0389 in |
| 18 | 2.000 | .0478 in | .0438 in | .0518 in |
| 16 | 2.500 | .0598 in | .0548 in | .0648 in |
| 14 | 3.125 | .0747 in | .0697 in | .0797 in |
| 12 | 4.375 | .1046 in | .0986 in | .1106 in |
Fig. 1-30: Standard Gage Uncoated Steel
(reproduced with permission from HVAC Duct Construction Standards, SMACNA, Appendix 2)
| Thickness in Inches | Weight | ||
| Nom. | Min. | Max. | lb/ft2 |
| .016 | .014 | .018 | .028 |
| .020 | .0175 | .0225 | .285 |
| .024 | .0215 | .0265 | .342 |
| .025 | .0225 | .0275 | .356 |
| .032 | .0295 | .0345 | .456 |
| .040 | .037 | .043 | .570 |
| .050 | .046 | .054 | .713 |
| .063 | .059 | .067 | .898 |
| .080 | .076 | .084 | 1.140 |
| .090 | .086 | .094 | 1.283 |
| .100 | .095 | .105 | 1.426 |
| .125 | .12 | .13 | 1.782 |
Fig. 1-31: Aluminum Alloy 3003-H14
(reproduced with permission from HVAC Duct Construction Standards, SMACNA, Appendix 3
| Gage | Thickness in Inches | Weight Nom lb/ft2 | ||
| Min | Max | Nom | ||
| 30 | .0127 | .0187 | .0157 | .656 |
| 28 | .0157 | .0217 | .0187 | .781 |
| 26 | .0187 | .0247 | .0217 | .906 |
| 24 | .0236 | .0316 | .0276 | 1.156 |
| 22 | .0296 | .0376 | .0336 | 1.406 |
| 20 | .0356 | .0436 | .0396 | 1.656 |
| 18 | .0466 | .0566 | .0516 | 2.156 |
| 16 | .0575 | .0695 | .0635 | 2.656 |
| 14 | .0705 | .0865 | .0785 | 3.281 |
Fig. 1-32: Galvanized Tolerances
(reproduced with permission from HVAC Duct Construction Standards, SMACNA, Appendix 4)
Rectangular Metal Duct Construction
Duct construction requirements are listed in Fig. 1-33 through Fig. 1-39, reproduced with permission from HVAC Duct Construction Standards, SMACNA, Tables 1-3 through 1-9, pp. 1-16 - 1-22. The program uses these tables to determine the gage and reinforcement required for the material used in a rectangular or oval duct section.
Since the greater dimension of a rectangular duct is more likely to deform, that dimension is assumed to be critical. A gage, reinforcement spacing and tie rod requirement corresponding to the working pressure in the duct is chosen from the table. The smaller dimension is analyzed using the gage and reinforcement chosen for the greater dimension.
You can use the override forms to specify the reinforcement spacing. If you specify an override, the program will check the table and determine the gage and reinforcement rigidity class for that spacing. If there is no gage for that spacing, your override will be ignored. The program will proceed to choose the appropriate gage, reinforcement spacing and tie rod requirement.
As Fig. 1-33 through Fig. 1-39 are based on galvanized steel, the program will first find the duct construction requirements for that material then find the equivalent construction requirements for other materials. For aluminum ducts, the thickness is determined from Fig. 1-40 while Fig. 1- 41 is used to determine the reinforcement.
| Duct Dimension (in.) | Duct Gauge (No Reinforcement) | Minimum Rigidity Class on Minimum Guage Duct | ||||||
| Re-inforcement Spacing | ||||||||
| 10' | 8' | 5' | 4' | 3' | 2-1/2' | 2 | ||
| 10 dn. | ↑ | |||||||
| 12 | ↑ | |||||||
| 14 | ↑ | |||||||
| 16 | ↑ | |||||||
| 18 | 26 ga. | |||||||
| 20 | 24 ga. | A-26 | → | → | → | → | → | → |
| 22 | 22 ga. | A-26 | → | → | → | → | → | → |
| 24 | 22 ga. | A-26 | → | → | → | → | → | → |
| 26 | 20 ga. | A-26 | → | → | → | → | → | → |
| 28 | 18 ga. | B-24 | B-26 | → | → | → | → | → |
| 30 | 18 ga. | B-24 | B-26 | → | → | → | → | → |
| 36 | 16 ga. | C-22 | C-24 | C-26 | → | → | → | → |
| 42 | D-20 | D-24 | D-26 | C-26 | → | → | → | |
| 48 | E-20 | D-22 | D-26 | → | → | → | → | |
| 54 | E-18 | E-20 | D-26 | → | → | → | → | |
| 60 | F-18 | F-20 | E-24 | E-26 | → | → | → | |
| 72 | H-16 F+rod | G-18 F+rod | F-22 | F-24 | → | → | → | |
| 84 | H-16 F+rod | H-22 +rod | G-24 F+rod | → | → | → | ||
| 96 | I-16 F+rod | H-20 F+rod | H-22 F+rod | → | → | → | ||
| 97 UP | H-18 | → | → | → | → | |||
Fig. 1-33: 1/2-inch W.G.
Rectangular duct reinforcement for 1/2" of water, positive and negative static pressure

Fig. 1-34: 1-inch W.G.
Rectangular duct reinforcement for 1" of water, positive and negative static pressure (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-4, p. 1-17)

Fig. 1-35: 2-inch W.G.
Rectangular duct reinforcement for 2" of water, positive and negative static pressure (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-5, p. 1-18)

Fig. 1-36: 3-inch W.G.
Rectangular duct reinforcement for 3" of water, positive and negative static pressure (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-6, p. 1-19)

Fig. 1-37: 4-inch W.G.
Rectangular duct reinforcement for 4" of water, positive static pressure (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-7, p. 1-20)

Fig. 1-38: 6-inch W.G.
Rectangular duct reinforcement for 6" of water, positive static pressure (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-8, p. 1-21)

Fig. 1-39: 10-inch W.G.
Rectangular duct reinforcement for 10" of water, positive static pressure (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-9, p. 1-22)
| Galvanized Steel | Commercial Size (in.) |
| 28 | .025 |
| 26 | .032 |
| 24 | .040 |
| 22 | .050 |
| 20 | .063 |
| 10 | 0.080 |
| 16 | .090 |
Fig. 1-40: Aluminum Commercial Sizes
Galvanized steel gauge conversion to aluminum sheet thickness (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-14, p. 1-32)
| Galvanized Rigidity Class | Aluminum Dimension per Galvanized Class |
| A | C |
| B | D |
| C | E |
| D | F |
| E | H |
| F | H |
| G | I |
| H | K |
Fig. 1-41: Rigidity Class Conversion
Galvanized steel rigidity conversion (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 1-15, p. 1-32)
Round Metal Duct Construction
Duct construction requirements for round galvanized steel and aluminum ducts are given in Fig. 1-42 and Fig. 1-43, reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 3-2 and 3-3, pp. 3-3, 3-4. These tables give the galvanized steel gauge and the aluminum commercial size as a function of static pressure, type of seam (spiral or longitudinal) and diameter. The program uses these tables to select the gage for round ducts.
| Duct Diameter in Inches | Maximum 2" w.g. Static Positive | Maximum 10" w.g. Static Positive | Maximum 2" w.g. Static Negative | |||
| Spiral Seam Gauge | Longitudi nal Seam Gauge | Spiral Seam Gauge | Longitudi nal Seam Gauge | Spiral Seam Gauge | Longitudi nal Seam Gauge | |
| 8 | 28 | 28 | 26 | 24 | 28 | 24 |
| 14 | 28 | 26 | 26 | 24 | 26 | 24 |
| 26 | 26 | 24 | 24 | 22 | 24 | 22 |
| 36 | 24 | 22 | 22 | 20 | 22 | 20 |
| 50 | 22 | 20 | 20 | 20 | 20 | 18 |
| 60 | 20 | 18 | 18 | 18 | 18 | 16 |
| 84 | 18 | 16 | 18 | 16 | 16 | 14 |
Fig. 1-42: Gauge Selection
Round duct gauge selection, galvanized steel (reproduced with permission from (reproduced with permission from , SMACNA, , SMACNA, Table 3-2, p. 3-3)
| Duct Diameter in Inches | Maximum 2" w.g. Static Positive | Maximum 2" w.g. Static Negative | ||
| Spiral Seam Gauge | Longitudinal Seam Gauge | Spiral Seam Gauge | Longitudinal Seam Gauge | |
| 8 | .025 | .032 | .025 | .040 |
| 14 | .025 | .032 | .032 | .040 |
| 26 | .032 | .040 | .040 | .050 |
| 36 | .040 | .050 | .050 | .063 |
| 50 | .050 | .063 | .063 | .080 |
| 60 | .063 | .080 | N.A. | .090 |
| 84 | N.A. | .090 | N.A. | N.A. |
Fig. 1-43: Aluminum Gauge Schedule
Aluminum round duct gauge schedule (reproduced with permission from HVAC Duct Construction Standards, SMACNA, Table 3-3, p. 3-4)
Quantity Takeoffs
Ductwork
Since the unit weight of all sheet-metal sheets is pounds per square foot of surface area, the program therefore calculates the surface area of all ductwork to be used.
The program then calculates the total weight of sheet-metal ductwork on the basis of gauge for fibrous ducts and commercial size for aluminum ducts. The one-inch thick fibrous glass ducts are estimated on a per square foot basis.
The program calculates the quantity of flexible ducts based on the diameter and linear foot of flexible ducts. Duct reinforcements are not included in the weights of the ductwork.
Lining and Insulation
The program calculates the lining and insulation quantity takeoff on a per square foot basis. Appendix Three: Duct Fittings
Figures and tables appearing in this appendix are reprinted with permission from HVAC Systems Duct Design, SMACNA, 1981. Use the table to identify the figure that corresponds to each keyword choice on the fittypes form.

Duct Cross Section to which Coefficient "C" is referred is at the top of each table. Negative numbers indicate that the static regain exceeds the dynamic pressure loss of the fitting.
Table 6-6 LOSS COEFFICIENTS, ELBOWS
Use the velocity pressure (Vp) of the upstream section. Fitting Loss (TP) = C x Vp
A. Elbow, Smooth Radius (Die Stamped), Round (2)
B. Elbow, Round, 3 to 5 pc -- 90o (2)

|
| |||||||||||||||||||||||
|
| |||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
D. Elbow, Rectangular, Mitered (15)

|
| |||||||||||||||||||||||||||||||||||||||||||||||
E. Elbow, Rectangular, Mitered with Converging or Diverging Flow (15)
|
| |||||||||||||||||||||||||||
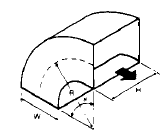
F. Elbow, Rectangular, Smooth Radius without Vanes (15)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
where: D = duct diameter, inches V = duct velocity, fpm
G. Elbow, Rectangular, Smooth Radius with Splitter Vanes (2)
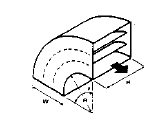
| NOTES FOR THIS FIGURE ONLY: A) See Page 5.12 to calculate splitter vane spacing. B) CR = Curve Ratio C) Use correction factors in Note 1 on Page 6.13 for elbows other than 90o. |

H. l Elbow, Rectangular, Mitered with Turning Vanes (2)
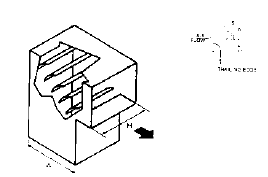
|
| ||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
I. Elbows, 90o, Rectangular, Z-Shaped (15)

|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Re = 8.56 D V
where: D= hydraulic diameter, inches V = duct velocity, fpm
J. Elbows, 90o, Rectangular in Different Planes (15)
|
| |||||||||||||||||||||||||||||||||
K. Elbows, 30o, Round, Offset (15)

|
| ||||||||||||||||||||||||
L. Elbows, 90o, Rectangular Wye or Tee Shape
Table 6-7 LOSS COEFFICIENTS TRANSITIONS (Diverging Flow)
Use the velocity pressure (Vp) of the upstream section. Fitting loss (TP) = C x Vp
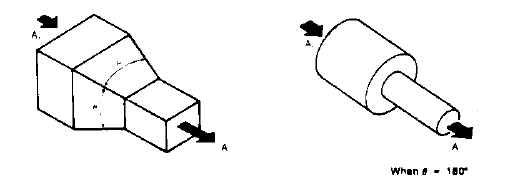
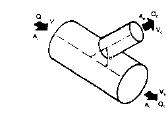
A. Transition, Round, Conical (15)
Re = 8.56 DV where: D = Upstream V = Upstream Velocity |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
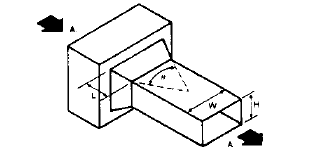
B. Transition, Rectangular, Pyramidal (15)

When ? = 180? |
| |||||||||||||||||||||||||||||||||||
Note 6: A = Area (Entering airstream), A1 = Area (Leaving airstream)
C. Transition, Round to Rectangular (15)
D. Transition, Rectangular to Round (15) | For Figures C and D, compute ? using the equations and find the coefficient C from Table 6- 7B. Transition, Rectangular, Pyramidial. |

E. Transition, Rectangular, Side Straight (15)
|
| |||||||||||||||||||||||||||||||
F. Transition, Symmetric at FanWith Duct Sides Straight (15)

|
| |||||||||||||||||||||
Note 6: A = Area (Entering airstream), A1 = Area (Leaving airstream)
G. Transition, Asymmetric at Fan with Duct Sides Straight, Top Level (15)
|
| |||||||||||||||||||||
H. Transition, Asymmetric at Fan With Duct Sides Straight, Top 10? Down (15)

|
| |||||||||||||||||||||
I. Transition, Asymmetric at Fan With Duct Sides Sgraight, Top 10? Up (15)

|
| |||||||||||||||||||||
Note 6: A = Area (Entering airstream), A1 = Area (Leaving airstream)
J. Transition, Pyramidal at FanWith Duct (15)
|
| |||||||||||||||||||||
Table 6-8 LOSS COEFFICIENTS TRANSITIONS (Converging Flow)
Use the velocity pressure (Vp) of the downstream section. Fitting loss (TP) = C x Vp
A. Contraction, Round and Rectangular, Gradual to Abrupt (15)
|
| |||||||||||||||||||||||||||||||
B. Contraction, Conical, Round and Rectangular (15)

| (See Note 7)
|
Co
| |||||||||||||||||||||||||||||
Note 7: A1 = Area (Entering airstream), A = Area (Leaving airstream)
C. Contraction, Rectangular Slot to Round (15)
|
| |||||||||||||||||||||||||||
Table 6-9 LOSS COEFFICIENTS, CONVERGING JUNCTIONS (Tees, Wyes)
Use the velocity pressure (Vb) of the downstream section. Fitting loss (TP) = C x Vb
A. Converging Wye, Round (2)
|
| ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Note 8: A = Area (sq. in.), Q = Airflow (cfm), V = Velocity (fpm)
B. Converging Tee, 90?, Round (15)
|
| ||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
C. Converging Tee, Round Branch to Rectangular Main
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D. Converging Tee, Rectangular Main and Branch
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
F. Converging Tee, 45? Entry Branch to Rectangular Main
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

G. Symmetrical Wye, Dovetail, Rectangular (15)
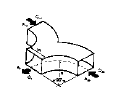
|
| ||||||||
H. Converging Wye, Rectangular (15)

|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I. Wye, Rectangular and Round (15)
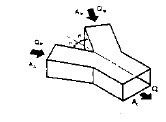
|
| |||||||||||||||||||||||||||||||||||||||||||||||
| When: A1b = A2b Ac = A1b + A2b | |||||||||||||||||||||||||||||||||||||||||||||||
Table 6-10 LOSS COEFFICIENTS, DIVERGING JUNCTIONS (Tees, Wyes)
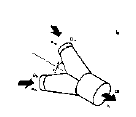
Use the velocity pressure (Vp) of the upstream section. Fitting loss (TP) = C x Vp
A. Tee or Wye, 30o to 90o, Round (15)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
B. 90o Conical Tee, Round (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
C. 45o Conical Wye, Round (2)
|
| ||||||||||||||||||||||||||||||||||||||||||||
D. 90o Tee, Round, Rolled 45o with 45o Elbow, Branch 90o to Main (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
E. 90o Tee, Round, with 90o Elbow, Branch 90o to Main (2)
|
| ||||||||||||||||||||||||||||||||||||||||||||
F. 90o Tee, Round, Rolled 45o with 60o Elbow, Branch 45o to Main (2)
|
| ||||||||||||||||||||||||||||||||||||||||||||
G. 90o Conical Tee, Round, Rolled 45o with 45o Elbow, Branch 90o to Main (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
H. 90o Conical Tee, Round, Rolled 45o with 60o Elbow, Branch 45o to Main (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
I. 45o Wye, Round, Rolled 45o with 60o Elbow, Branch 90o to Main (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
J. 45o Conical Wye, Round, Rolled 45o with 60o Elbow, Branch 90o to Main (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
K. 45o Wye, Round, Rolled 45o with 30o Elbow, Branch 45o to Main (2)

|
| ||||||||||||||||||||||||||||||||||||||||||||
L. 45o Conical Wye, Round, Rolled 45o with 30o Elbow, Branch 45o to Main (2)
|
| ||||||||||||||||||||||||||||||||||||||||||||
M. 45o Wye, Conical Main and Branch with 45o Elbow, Branch 90o to Main (15)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
N. Tee, 45o Entry, Rectangular Main and Branch
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
P. Tee, 45o Entry, Rectangular Main and Branch with Damper

|
| |||||||||||||||||||||||||||||||||||||||||||||||||
Q. Tee, Rectangular Main and Branch
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
R. Tee, Rectangular Main and Branch with Damper
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
S. Tee, Rectangular Main and Branch with Extractor

|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T. Tee, Rectangular Main to Round Branch
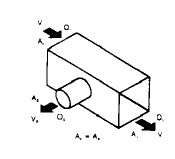
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
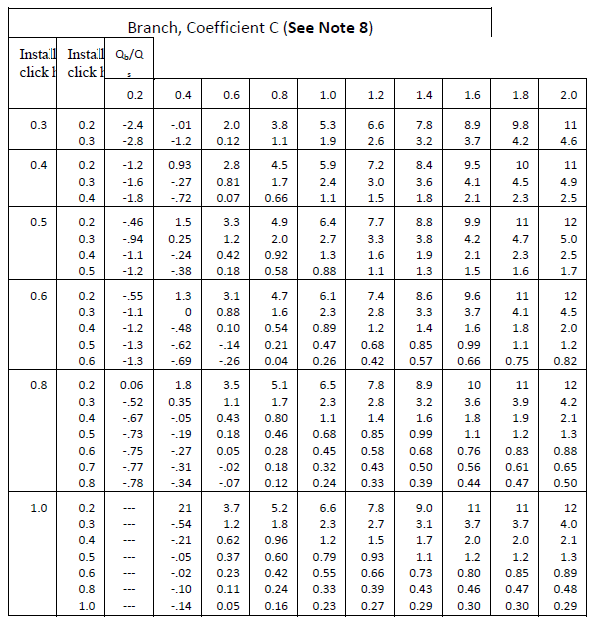
| Branch, Coefficient C (See Note 8) | |||||||||||||
| o | Vb/Vc | ||||||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | |
| 15 30 45 60 90 | 0.81 0.84 0.87 0.90 1.0 | 0.65 0.69 0.74 0.82 1.0 | 0.51 0.56 0.63 0.79 1.0 | 0.38 0.44 0.54 0.66 1.0 | 0.23 0.34 0.45 0.59 1.0 | 0.20 0.26 0.38 0.53 1.0 | 0.11 0.19 0.29 0.43 1.0 | 0.06 0.15 0.24 0.36 1.0 | 0.14 0.15 0.23 0.33 1.0 | 0.30 0.30 0.30 0.39 1.0 | 0.51 0.51 0.51 0.51 1.0 | 0.76 0.76 0.76 0.76 1.0 | 1.0 1.0 1.0 1.0 1.0 |
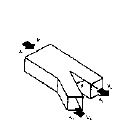
|
| ||||||||||||||||||||||||||||||||||
V. Tee Rectangular Main to Conical Branch (2)

|
| ||||||||||||||||||||||||||||
W. Wye, Rectangular (15)
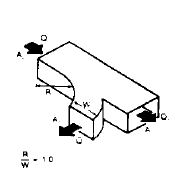
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X. Symmetrical Wye, Dovetail, Rectangular (15)
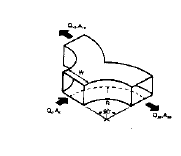
|
| |||||||||