Building Loads Analysis Program
Copyright 1998 Skidmore, Owings & Merrill. All rights reserved.
Overview
This manual describes methods for estimating and analyzing the heating and cooling requirements of a building model. These estimates determine the performance requirements for the HVAC equipment that will maintain design air conditions within the building.
Computer programs for estimating building loads can analyze and compare several alternative systems and equipment.
Loads program features can include:
A User Interface of forms, windows, menus, and commands to describe the building
Built-in Reference Libraries (databases) consisting of:
- Fixed Information that can be used on any project
- Project-Specific Information that can be customized from the Fixed Information
- Project-Specific Information that can be entered directly through input forms
Generation of weather data for a project site using location data
Five-level structure of the thermal model which include:
- Terminals (diffusers, registers, grilles, radiators, convectors, etc.)
- Rooms (spaces that are separated from each other by physical barriers or by function)
- Zones (rooms served by a thermostat or grouped together for a tenant)
- Systems (zones served by the same air handling unit, heating system, or cooling system)
- Plants (primary heating & cooling equipment that serve systems and secondary equipment)
Duplication of rooms using master room internal and exposure loads
Calculation of year-round cooling loads and air quantities
Calculation of winter heating loads and air quantities
Systems Analysis
- All Air systems (Constant or Variable Air Volume with or without reheat)
- Air and Water systems
- All Water systems
- Special systems (thermal storage, heat recovery, etc.)
Cooling load optimization by rotating the building orientation
Reference Libraries
The manual provides some of the information databases that are built into loads programs or are required for using such computer programs.
These libraries contain properties and performance characteristics of building materials, weather conditions for different locations, and space, system, and equipment design criteria.
Fixed Information Library
The fixed information library consists of information that do not change, or can only be changed by the source that provided the change, and is independent of a specific project. It includes:
- Cooling Load Factors (CLF) for Glass, Lights, People, and Equipment
- Cooling Load Temperature Differences (CLTD)
- CLTD Corrections for Latitude and Month applied to Walls and Roofs
User-Defined Library
The user-definable library is a flexible data base of properties and performance capabilities reflecting the professional judgment and experience of the engineer.
Examples of the tables in the user-definable reference library are
- Location data for different cities
- Typical 24-hour profiles for lighting, occupancy, building operation, etc
- Thermal and physical properties of typical floors, doors, walls, etc.
Because this library is under your control, you can ensure that it complies with appropriate regulatory codes and standards. You can use sources such as ASHRAE standards 55-1981 and 62-1981 to help build the tables in this library. You can add to these sources with current codes and standards for building types such as hospitals, schools, and industrial facilities.
By enhancing and expanding this library you can
- develop master data for building sections appropriate to your practice
- develop design criteria for different types of rooms
- set the design standards for your practice
Project-Specific Library
As you describe a building model, you will draw upon the information in the user-definable library to assemble and tailor a project-specific library that reflects a particular design solution.
The project-specific library contains thermal and physical properties of: Ceilings, doors, floors, partitions, roofs, rooms, skylights, walls, windows, usage profiles
You can build a project-specific library description by
- adding a standard description from the user-definable library
- modifying any portion of the standard description in the project-specific library
- entering a new description into the project-specific library
Generating Weather Data
A Loads Program can generate 24-hour weather conditions for a design day of the month. It can also calculate solar heat gain factors for any hour of the year at the specified project location.
Structure
The hierarchical organization of the thermal building model in the Loads Program consists of rooms, zones, systems, and plants.
The room is the basic unit of space in the building. It requires no further subdivision in terms of space usage and treatment by HVAC equipment.
- You analyze each room for internal and external loads and compliance with standards you can define.
- You can use the room loads and air quantities calculated by the Loads Program to select room conditioning equipment, and to design the ductwork and piping systems for the building.
Rooms are grouped together to form zones. Examples of zones are rooms controlled by the same thermostat and rooms served by the same VAV terminal box or tenant.
The system level of the model consists of groups of zones served by an Air Handling Unit (AHU). The Loads Program analyzes systems to determine the heating and simultaneous peak cooling loads at the coils in the Air Handling Unit.
The Loads Program combines all the systems defined in the model to obtain the heating and cooling loads at the plant level. You can use the plant loads to select the primary equipment for the building, such as chillers and boilers.
Duplicate Rooms
In any large building model, there are numerous rooms that have identical internal loads, dimensions, and exterior exposures. The Loads Program allows you to use one of these rooms as a master from which you can make duplicate rooms. The duplicate rooms will be identical to the master room, except for zone assignment and floor number.
Once you add a duplicate room to your project, you can change it any time by
- using a different master room to define the duplicate room, or
- changing the internal loads and/or exterior exposures of the master room
Year-Round Cooling Loads
The Loads Program determines the peak cooling load of each room and the simultaneous peak cooling loads at the zone, system, and plant levels. The CLDT/CLF method is used to calculate external and internal room loads through glass, roofs, and walls.
Winter Heating Loads
Winter heating loads calculations are based on the design month and hour for the project location. Winter heating loads include infiltration, transmission, and ventilation. The Loads Program performs heat loss/gain calculations for all external/internal load sources at the design month and hour.
System Analysis
The System Analysis feature of the Loads Program consists of analyzing the air flow for an air conditioning system.
- The analysis begins at the leaving side of the apparatus (cooling or heating coil).
- It continues through the supply duct, rooms, return plenum and ductwork, and return and supply fans.
- It terminates at the entering side of the apparatus.
Options
The Loads Program furnishes you with a variety of options when you perform a system analysis. With these options, you can specify:
Minimum supply and outdoor air quantities for different types of rooms using:
- air changes per hour
- air quantity per person
- air quantity per unit area
Pressure differential required between a room and its surrounding space
Type of extract system for any room, such as return or exhaust
Percent outdoor air of the system using either
- the room with the highest percent outdoor air
- the average percent outdoor air of all rooms in the zone
Ducted or plenum return for any room
Summer and winter supply air temperatures
You may define an AHU having characteristics that are identical to an existing AHU in the project.
To reduce the effort of entering duplicate information, you can request the Loads Program to make a duplicate of the original AHU and add it to the project-specific library. This same feature applies to zones.
Results
The results generated by the System Analysis feature include:
Summer air quantities for
- rooms at their peak loads
- zones and systems at their simultaneous peak loads
Supply air quantities and temperatures that account for
- minimum air requirements
- summer and winter air quantities based on loads
Zone Reheat loads for summer
Ceiling plenum temperatures
Quantities and conditions for return, outdoor, mix, and supply air in the system
Simultaneous peak system cooling load based on psychometric analysis
The Loads Program analyzes specific system types, such as constant volume and variable air volume, with or without primary and zone reheat, using the features described above.
Building Rotation
The orientation of a building on its site can greatly affect the requirements for the heating and cooling equipment. A feature of the Loads Program allows you to change the angle of orientation for the building. You can then produce supplemental analyses to compare different orientation schemes.
Reports
The Loads Program can produce up to fourteen reports for each project. Before you request an analysis, you can choose which reports you want the Loads Program to generate.
The reports contain listings of project information that you enter, as well as the results of calculations by the program. When a report presents information for project elements such as rooms, the rooms are grouped first by system, then zone. Within the zone, the rooms are sorted by project identification number. Information for zones is grouped by system and sorted within the system by zone identification number.
Input Echo
This report summarizes the information in the fields on the data forms and through the use of commands.
Room Summary
This report includes
- general room information
- sensible, latent, and total heat gains
- month and hour of peak load for each room
- transmission and infiltration heating losses
- total supply, return, and exhaust air quantities
- room and supply air temperatures at peak and winter conditions
Zone Summary
This report includes
- general zone information
- month and hour of peak load for each zone
- transmission and infiltration heating loads
- supply air quantities for each zone
- supply air temperature for summer and winter
- latent and sensible heat gains
- number of duplicate zones, if any
- winter excess heating
- zone reheat, if any
Zone information is used to size secondary air conditioning equipment such as terminal boxes.
System Summary
This report presents information for each AHU in the project. The data in the report includes
- peak month and hour for each AHU
- total latent and sensible heat gains
- transmission, infiltration, and ventilation heating loads
- humidification
- winter cfm
- supply and return air quantities
- percent outdoor air
- total required cooling load
- cooling coil air conditions
- number of duplicate Air Handling Units, if any
Room Design Criteria
This report presents information for each room, such as
- zone number
- indoor design temperatures and relative humidities
- supply and outdoor air values
- type of extraction
- occupancy, equipment, and lighting densities
Room Internal Heat Gains
This report includes
- month and hour of peak load for each room
- sensible and latent heat gains from occupants, equipment, and lighting
- occupancy, equipment, and lighting densities
- total room sensible and latent heat gains
Room External Heat Gains
Room heat gains through the the shell elements used in constructing the room are:
- windows and skylights
transmission and solar - roofs and walls
transmission and solar - doors, floors, and partitions
transmission - windows, doors, and skylights
total infiltration quantities and sensible and latent heat gain
Room Winter Heat Losses
Winter heating loads include transmission losses through:
- doors
- floors
- partitions
- roofs
- skylights
- walls
- windows
Winter heating loads also include:
- infiltration air heat losses due to windows, skylights, doors, and other room elements
- total winter transmission and infiltration losses due to room elements
- internal and solar heat gains that offset the transmission and infiltration losses
Room Air Quantities and Temperatures
The reports show the supply, outdoor and extract air quantities for each room. Also included are the temperatures for room air and supply air at room peak conditions and during winter.
Supply air information includes:
- minimum, summer, and winter cfm
- air changes per hour
- cfm per person and per square foot
Outdoor air information includes:
- quantity
- percent of supply air
- air changes per hour
- cfm per person and per square foot
Extract (return and exhaust) air information include:
- return quantity
- exhaust quantity
- percent of supply
The program reports the room air temperature and supply air temperature, as well as the difference between the two for room peak and winter conditions.
Room Detail
This report presents information for each room, including
- general room data
- heating and cooling loads
- exposure data
- air data, including
- supply, infiltration, exhaust, and return air quantities
- supply and return air temperatures
- check values
- load peaks
Zone Detail
This report presents information for each zone, including
- general zone information
- internal and external loads due to each room in the zone
- heat gains and losses for internal and external loads
- air data
System Detail
This report presents the information for each system, including
- cooling coil psychrometrics
- heating and cooling system loads and air quantities
- heat losses and gains for internal and external loads
- air data
Plant Summary
This report presents the simultaneous peak heating and cooling loads of all the systems. These loads represent the capacities of the primary equipment such as:
- boilers,
- chillers,
- heat exchangers
- cooling towers.
The summary includes
- the total floor area served by the primary equipment
- heating and cooling loads at peak hour
- month and hour of peak cooling
- total air quantities for the system
- heating gains and losses for all internal and external loads
Project Weather and Solar Data
This report presents weather data for a typical design day during each summer and winter month you request the Loads Program to perform an analysis. When a room contains skylights or windows with a non-zero tilt, the report provides solar factors for the skylight or window exposures.
Building Construction with Information Libraries

Reference Library is for All Projects. Project is for Specific Project (override Reference)

Building Materials Libraries is for All Architectural-Engineering Disciplines

Building Materials Wall Library by Architectural-Engineering Discipline

Building Materials Wall Library for HVAC Discipline

Users can create additional Reference Libraries for Building Materials & Systems

Room Construction with Libraries (Edit for Specific Project)

Room Construction with Libraries (Edit for Specific Project)

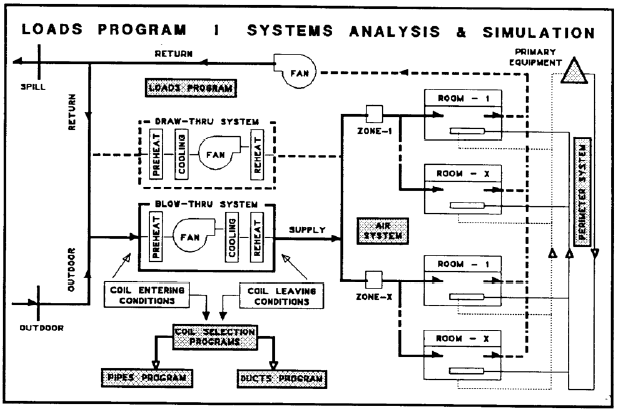
SYSTEMS, ZONES and ROOMS Organization

The Building Model can be simulated for Typical Days of Month OR Every Day of Year
Engineering Basis
Building Systems Organization and Structure
The hierarchical building organization for the Loads Program consists of four levels: rooms, zones, systems, and plants.
Fig. 1-1 shows the pyramid structure of rooms, zones, systems, and plants. The Loads Program uses this structure to organize input data, determine the sequence of calculations, and organize and present out reports.

Figure 1.1
Fig. 1-2 is an example of the grouping of rooms into zones and zones into Air Handling Unit (AHU) systems. Groups of Air Handling Units are served by chillers and boilers which are considered the plant.


Fig 1.2

Rooms
A room is the basic unit of space in the building. Rooms are defined by the engineer and require no further subdivision in terms of space usage and treatment by HVAC equipment. The Loads Program analyzes each room in detail for internal and external loads, and for userdefined criteria. Rooms are constructed with the information from the reference library along with physical dimensions entered on data forms.

Fig. 1-3 shows how engineering and dimensional data are used to construct rooms.
Zones
Rooms are grouped together to form zones. Examples of zones are rooms served by the same VAV terminal box or tenant. The zones in Fig. 1-2 are the rooms served by the same VAV box.
System
Systems are groups of zones. The system is the air handling unit. The system is analyzed psychrometrically to obtain the loads at the primary heating and cooling coils.

Plant
Systems are combined and served by plants. The plant load is the load of the primary equipment (boilers, chillers, cooling towers, and heat exchangers).

Weather Data Factors
Climatic data required for load calculations are the dry-bulb temperature (DB) and the wet-bulb temperature (WB). Sky or cloud cover (SC) is required to estimate energy loads and is assumed to be 0 (cloudless) for design load calculations.
Hourly DB and WB temperatures for design load calculations are generated by the Loads Program using the design conditions for the location. These temperatures are estimated by fitting sinusoidal curves between:
- the minimum and maximum design conditions for each month and
- the minimum and maximum values for the day to obtain hourly temperatures
Fig. 1-4 shows the curve that generates the design DB and WB temperatures for each month. To generate this curve, it is necessary to enter
- summer design DB and WB temperatures
- winter design DB temperatures
- summer and winter design months

The generated DB and WB temperatures are used to calculate the summer infiltration and ventilation loads for any given hour.
Heat gain due to conduction through glass, walls, and roofs is calculated using the Cooling Load Temperature Difference (CLTD) method as described in the ASHRAE Handbook: 1985 Fundamentals.
The Design Temperature Difference method is used to calculate the heat gains through partitions, ceilings, and floors.
The Cooling Load Factors (CLF) method from ASHRAE is used to calculate internal loads from lights, people, appliances, and solar heat gains through glass.
Hourly Outside Temperatures
The equations used to determine design temperatures are:

| where | x | = | given month number |
| x1 | = | period for 1st cycle | |
| x2 | = | period for 2nd cycle | |
| T1 | = | temperatures at given month x for 1st cycle | |
| T2 | = | temperatures at given month x for 2nd cycle | |
| y | = | amplitude = yearly temperature range | |
| Ms | = | summer design month numbers | |
| Mw | = | winter design month numbers | |
| Tmax | = | summer design temperature at month number Ms | |
| Tmin | = | winter design temperature at month number Mw |
Table 1 is used to calculate the hourly temperatures for each month
| Table 1 | Percentage of Daily Range | ||||||
| Time,h | % | Time,h | % | Time,h | % | Time,h | % |
| 1 | 87 | 7 | 93 | 13 | 11 | 19 | 34 |
| 2 | 92 | 8 | 84 | 14 | 3 | 20 | 47 |
| 3 | 96 | 9 | 71 | 15 | 0 | 21 | 58 |
| 4 | 99 | 10 | 56 | 16 | 3 | 22 | 68 |
| 5 | 100 | 11 | 39 | 17 | 10 | 23 | 76 |
| 6 | 98 | 12 | 23 | 18 | 21 | 24 | 82 |
| (ASHRAE Fundamentals 26.7) | |||||||
The temperature for the current hour and month is given by
Thour= Design DBmonth - (Daily Range × Percenthour )
| where: | Design DBmonth | = | Design Dry-Bulb temperature for the month |
| Daily Range | = | Daily Range for the location | |
| Percenthour | = | percent of daily range at the current hour from Table 1 |
Solar Data Factors
| Data: | L: | Latitude, degrees | + | = | North |
| - | = | South | |||
| I: | Longitude, degrees | + | = | West | |
| - | = | East |
| TZN: | Time zone number, (hours behind Greenwich mean time) (See Figure 1-5 and Table 2) |
| d: | Date, days (from start of year), (1-366) |
| t: | Time, hours (after midnight), (0-24) |
| DST: | Daylight saving time indicator, (output of DST) 0 for standard time and 1 for daylight saving time |
| p: | Ground reflectivity |
| CN: | Clearness number (see Figure 1-6) |
| CCF: | Cloud Cover Factor |
| ITHC: | Total solar radiation calculated for a horizontal surface under a cloudy sky of given cloud amount and types of cloud. |
| ITH: | Total solar radiation calculated for a horizontal surface under a cloudless sky at the same solar hour as of ITHC. |
| IS: | Season Index |
| CAj: | Cloud amount at the j-th layer where j = 1, 2, 3, and 4. |
| TOCj: | Type of cloud at the j-th layer, where j = 1, 2, 3, and 4. |
| TCA: | Total cloud amount |
| P: | Cloudless sky factor in Table 5 shown in the CCF routine |
| C: | Standard diffuse sky factor from Tables 3 and 4 in the SUN routine. |
| CC: | Cloud cover calculated in the CCF routine |
| CCF: | Cloud cover factor determined by the CCF routine |
| WA: | Azimuth angle of the surface under consideration in radians from south; (+) if west and (-) if east of south |
| WT: | Tilt angle of the surface under consideration in radians from the horizontal surface; zero for the horizontal surface and c/2 for the vertical walls |
cos (Z), cos (W) and cos (S): Direction cosines of direct radiation (calculated in SUN)
| IDN: | Intensity of direct solar radiation for cloudless condition, Btu/h sq ft |
| BS: | Diffuse radiation from the cloudless sky, Btu/h sq ft (calculated in SUN) |
| BG: | Diffuse radiation from the ground, BTU/h sq ft (calculated in SUN) |
| SALT: | Solar altitude angle in radians (calculated in SUN) |
| (ASHRAE Procedure) | |
(reprinted by permission from the Procedure for Determining Heating and Cooling Loads for Computerizing Energy Calculations, ASHRAE, 1975)
| Table 2 | |
| Time Zone Number in U.S. for Standard Time | TZN |
| Atlantic | 4 |
| Eastern | 5 |
| Central | 6 |
| Mountain | 7 |
| Pacific | 8 |
| (ASHRAE Procedure) | |

(reprinted by permission from the Procedure for Determining Heating and Cooling Loads for Computerizing Energy Calculations, ASHRAE, 1975)

(reprinted by permission from the Procedure for Determining Heating and Cooling Loads for Computerizing Energy Calculations, ASHRAE, 1975)

(reprinted by permission from the Procedure for Determining Heating and Cooling Loads for Computerizing Energy Calculations, ASHRAE, 1975)
| Table 3: Values of *, ET, A, B, and C for Northern Hemisphere | |||||
| A | B | C | |||
| Date | Declination | ET (Hours) | BTU | Air-1 | |
| Jan. 21 | -20.0 | -.190 | 390 | 0.142 | 0.058 |
| Feb. 21 | -10.8 | -.230 | 385 | 0.144 | 0.060 |
| Mar. 21 | 0.0 | -.123 | 376 | 0.156 | 0.071 |
| Apr. 21 | 11.6 | .020 | 360 | 0.180 | 0.097 |
| May 21 | 20.0 | .060 | 350 | 0.196 | 0.121 |
| June 21 | 23.45 | -.025 | 345 | 0.205 | 0.134 |
| July 21 | 20.6 | -.103 | 344 | 0.207 | 0.136 |
| Aug. 21 | 12.3 | -.051 | 351 | 0.201 | 0.122 |
| Sep. 21 | 0.0 | .113 | 365 | 0.177 | 0.092 |
| Oct. 21 | -10.5 | .255 | 378 | 0.160 | 0.073 |
| Nov. 21 | -19.8 | .235 | 387 | 0.149 | 0.063 |
| Dec. 21 | -23.45 | .033 | 391 | 0.142 | 0.057 |
| (ASHRAE Procedure) | |||||
Tables 3 and 4 list, as a function of date, the declination angle, ?; the equation of time, ET; the apparent solar constant, A; the atmosphere extinction coefficient, B; and sky diffuse factor, C.
| Table 4: Values of *, ET, A, B, and C for Northern Hemisphere | |||||
| A | B | C | |||
| Date | Declination | ET (Hours) | BTU | Air-1 | |
| Jan. 21 | -20.0 | -.190 | 390 | 0.207 | 0.136 |
| Feb. 21 | -10.8 | -.230 | 385 | 0.201 | 0.122 |
| Mar. 21 | 0.0 | -.123 | 376 | 0.177 | 0.092 |
| Apr. 21 | 11.6 | .020 | 360 | 0.160 | 0.073 |
| May 21 | 20.0 | .060 | 350 | 0.149 | 0.063 |
| June 21 | 23.45 | -.025 | 345 | 0.142 | 0.057 |
| July 21 | 20.6 | -.103 | 344 | 0.142 | 0.058 |
| Aug. 21 | 12.3 | -.051 | 351 | 0.144 | 0.060 |
| Sep. 21 | 0.0 | .113 | 365 | 0.156 | 0.071 |
| Oct. 21 | -10.5 | .255 | 378 | 0.180 | 0.097 |
| Nov. 21 | -19.8 | .235 | 387 | 0.196 | 0.121 |
| Dec. 21 | -23.45 | .033 | 391 | 0.205 | 0.134 |
| (ASHRAE Procedure) | |||||
Calculation Sequence
1. Determine ?, ET, A, B, and C from Table 3.
2. h' = cos-1 (-tan(L)tan(?))(see Figure 1-7).

4. Sunrise time (SRT) and sunset time (SST), hour, (1-24)

5. Hour angle, h in degrees.
h = 15 (t - 12 + TZN + ET) - longitude
if h > h', skip all the remaining calculations in this sequence then set
IDN = 0 BS = 0 BG = 0
6. Direction cosines of direct solar beam

7. Solar altitude angle, SALT, in radians.

8. Solar azimuth angle, SAZM, in radians.

9. Intensity of direct solar radiation for a cloudless condition

10. Diffuse sky radiation (sky brightness) for a cloudless condition.

11. Ground reflected radiation for a cloudless condition (ground brightness)

Calculation Modification for Southern Hemisphere
The preceding algorithm is applicable to the northern hemisphere only. For buildings in the southern hemisphere, these modifications are required:
1. Shift values of B and C in Table 3 by six months. Values of ?, ET, A, B and C for the southern hemisphere are shown in Table 4.

Calculation Sequence

| Table 5: Values of P, Q, and R | |||
| Season | P | Q | R |
| Spring | 1.06 | 0.012 | -0.0084 |
| Summer | 0.96 | 0.033 | -0.0106 |
| Autumn | 0.95 | 0.030 | -0.0108 |
| Winter | 1.14 | 0.003 | -0.0082 |
| (ASHRAE Procedure) | |||
The value of P is the cloudless sky factor. It depends on the proportion of direct to diffuse sky radiation in reference to the standard values published in the ASHRAE Handbook: 1972 Fundamentals.
If the value of P is unity, the proportion of direct to diffuse solar radiation causes the solar radiation evaluated for a horizontal surface under a cloudless sky to be equal to the value obtained by the method described in the ASHRAE Handbook: 1972 Fundamentals. If the value of P is different from unity, the direct to diffuse proportion is different from the standard values.
Calculation Sequence

4. Direct radiation on a horizontal surface under a cloudless sky.
IDh = IDN cos(Z )
5. Diffuse radiation on a horizontal surface under a cloudless sky.
IDh= BS
6. Total radiation on a horizontal surface under a cloudless sky.
ITH = IDH + Idh
7. Direct radiation on a horizontal surface under a cloudy sky.

8. Direction cosines of the normal to the surface under consideration (the surface has an azimuth angle of WA and a tilt angle of WT).
α=cos(WT )
β=sin(WA) xsin(WT )
γ=cos(WA) xsin(WT )
9. Cosine of the incident radiation on the surface under consideration.
cos(c)=α cos(Z ) + β cos(W ) + γ cos(S )
10. Direct radiation on a surface under consideration under a cloudless sky.
ID = IDN cos(π )
ID = 0 if cos( π ) < 0
11. Direct radiation on a surface under a cloudy sky.

12. Diffuse radiation for a cloudless sky.
Id = BS, for the horizontal surface.
Id = BS xY + BG/2, for the vertical surfaces
where
Y = 0.55 + 0.437 xU + 0.313 U2
U = cos( π )
If U < - 0.2, Y = 0.45
13. Diffuse radiation upon a horizontal surface under a cloudy sky.

Note: Diffuse radiation data for surfaces other than vertical and horizontal ones have not been analyzed sufficiently to date to provide a calculation procedure.
14. Diffuse radiation on a surface under consideration.

15. Total radiation upon a surface under a cloud sky.
ITC = IDC + IdC
When the cloud cover, CC is zero, then
ITC = IT = ID + Id
(ASHRAE Procedure)
Psychrometrics
Algorithms for Psychometric Calculations
These symbols are used throughout the psychrometric subroutines:
| DB: | Dry-bulb temperature, F |
| DP: | Dewpoint temperature, F |
| WB: | Wet-bulb temperature, F |
| t: | Temperature, either DB, WB, or DP, F |
| PD: | Barometric pressure, in. Hg |
| H: | Enthalpy of moist air, Btu/lb of dry air |
| HS: | Enthalpy of moist air saturated with water vapor, Btu/lb of dry air |
| PV: | Partial pressure of water vapor in moist air, in. Hg |
| PVS: | Partial pressure of water vapor in moisture saturated air, in. Hg |
| V: | Volume of moist air, cu ft/lb of dry air |
| W: | Humidity ratio of moist air, lb of water vapor per lb dry air |
| Ln(x): | Natural logarithm of x |
| Log10(x): | Common logarithm of x. |
These algorithms are used for calculating the psychrometric properties of moist air. They are present here in a package and can be applied to a variety of engineering applications.
a. PVS (T)
1. Let A1 = -7.90298 and B1 = -9.09718
A2 = 5.02808 and B2 = -3.56654
A3 = -1.3816-7 and B3 = 0.876793
A4 = 11.344 and B4 = 0.0060273
A5 = 8.1328-3
A6 = -3.49149

If T is less than 273.16, go to 3
Otherwise,

P 1 = A1 (z - 1)
P 2 = A2 (Log 10 (z )
P 3 = A3 [10 A4(1 - 1/2) - 1]
P 4 = a5 [10 A6(z - 1) - 1]
Go to 4.

P1 = B1 (z - 1)

P4 = Log10(B4)
4. PVS=29.921 x[10(P1+P2+P3+P4)]
b. PV (DB, WB, PB)

c. W (DB, WB, PB)
d. H (DB,WB, PB)
H = 0.24 xDB + (1061 + 0.444 xDB ) xW (DB,WB, PB )
e. V (DB, WB, PB)
1. W V =W (DB,WB, PB )

f. H (DP, DP, PB)

2. H = 0.24 xDB +(1061 +0.444 xDB ) xW
g. WB (H, PB)
1. If PB= 29.92 and H > 0
Let Y = Ln(H )
For H < 11.758
WB=0.6040 + 3.4841 xY +1.3601 xY 2 +0.9731 xY 3
For H > 11.758
WB=30.9185 - 39.682 xY + 20.5841 xY2 - 1.758 xY3
If PB does not equal 29.92, or H≤ 0, solve this equation by iterating WB.
H =0.24 xWB +(1061 +0.444 xWB ) xW (WB,WB,PB )
h. DP (PV)
1. Let Y = Ln(PV )
If PV <0.18036
DP=71.98 + 24.873 xY +0.8927xY2
Otherwise,
DP=79.047 + 20.579 xY +1.8893 xY2
(ASHRARE Procedure)
Cooling Loads
Space Envelope Loads
The Loads Program calculates external heat gain loads from the following sources:
- Glass
- Walls
- Roofs
- Doors
- Windows
- Skylights
- Floors
- Partitions
- Ceilings
- Infiltration
Heat Gain Through Glass
The solar heat gain factors (SHGF) tabulated in the ASHRAE Handbook: 1985 Fundamentals are for 1/8-inch thick, regular sheet single glass and are obtained from these equations:

| where: | π | = transmitted component of solar heat gain |
| α | = absorbed component of solar heat gain | |
| ID | = direct solar radiation on a given surface | |
| Id | = diffuse solar radiation on a given surface | |
| θ | = angle of incidence on a given surface | |
| tj | = polynominal coefficients for transmission | |
| aj | = polynominal coefficients for absorptance |
The polynominal coefficients aj and tj for 1/8-inch single glass are shown in Table 6. Fig. 1-9 shows the flow of solar radiation through glass. (π and α are the transmittance and absorption factors).
| Table 6:Absorptance and Transmittance Coefficients for Glass | ||
| j | Absorptance Coefficient aj | Transmittance Coefficient tj |
| 0 | 0.01154 | -0.00885 |
| 1 | 0.77674 | 2.71235 |
| 2 | -3.94657 | -0.62062 |
| 3 | 8.57881 | -7.07329 |
| 4 | -8.38135 | 9.75995 |
| 5 | 3.01188 | -3.89922 |
| (ASHRAE Fundamentals) | ||

and:
| SHGF | = Solar Heat Gain Factor |
| T | = transmitted component of solar heat gain |
| α | = absorbed component of solar heat gain |
| M1 | = inward flow fraction of absorbed radiation |
| h1 | = inside surface heat transfer coefficient |
| h0 | = outside surface heat transfer coefficient |
The Loads Program assumes still air on the inside (h1 = 1.40) and 7.5 mph wind on the outside (h0 = 4.0). N, is, therefore, assumed to be 0.267 throughout the year.
Transmittance and absorptance coefficients for other types of glass are available. However, as an approximation, the solar heat gain factor for 1/8-inch single-glass is multiplied by the shading coefficient for the other glass types to obtain the solar heat gain. The shading coefficient factor allows for reflected radiation. Therefore, the shading coefficient for 1/8-inch double-sheet glass is 1. The solar radiation heat gain through glass is:
Qrg= Ag x SC x SHGFmax x CLF
| Ag | = glass area, sq ft |
| Ogr | = radiation gain through glass, Btu/h |
| SC | = shading coefficient |
| SHGFmax | = maximum value of solar heat gain factor during 24-hour period for given orientation and 1/8-inch single-sheet glass |
| CLF | = cooling load factor for given orientation and room construction |
The conducted heat gain through glass is:
Qcg= AgUg CLTD
| where: | Qcg | = conducted heat gain through glass, Btu/h |
| Ag | = glass area, sq ft | |
| Ug | = heat transmission coefficient of glass, Btu/h sq ft F | |
| CLTD | = Cooling Load Temperature Difference, F |
| Table 7: Cooling Load Temperature Differences (CLTD) | ||||||||||||
| Hour (AM) | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 |
| CLTD | 1 | 0 | -1 | -2 | -2 | -2 | -2 | 0 | 2 | 4 | 7 | 9 |
| Hour (PM) | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| CLTD | 12 | 13 | 14 | 14 | 13 | 12 | 10 | 8 | 6 | 4 | 3 | 2 |
| (ASHRAE Fundamentals 26.14) | ||||||||||||
The values in Table 7 were calculated for an inside temperature 78oF, an outdoor maximum temperature of 95oF, and an outdoor daily range of 21oF. The table is used for outdoor maximums between 93oF and 102oF provided the daily average temperature is 85oF.
Corrections to CLTD values can be made in accordance with the guidelines in Chapter 26 of the ASHRAE Handbook: 1981 Fundamentals. These include corrections for outside conditions, color, location, orientation, and inside temperatures.
Table 8 shows corrections to the CLTD values for indoor temperatures other than 78oF and Table 9 shows corrections for different combinations of daily range and design outdoor air temperatures.
| Table 8: CLTD Corrected for Inside Conditions | |||||||||
| Inside DB (oF) | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| Correction (oF) | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 |
| (ASHRAE Manual) | |||||||||
| Table 9: CLTD Corrected for Latitude and Month Conditions Heat Gain Through Walls and Roofs | ||||||||||||||
| Outdoor Air Design F) | Daily Range (F) | |||||||||||||
| 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | |
| 88 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | -12 | -13 | -14 | -15 |
| 90 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | -12 | -13 |
| 92 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 |
| 94 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 |
| 96 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| 98 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | -5 |
| 100 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
| 102 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 |
| 104 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 106 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
| (ASHRAE Manual) | ||||||||||||||
The heat gain through a wall or roof consists of a transmission gain due to the temperature difference between indoors and outdoors and a heat gain resulting from the intensity of solar radiation striking the outside surface. The net heat gain is affected slightly by the wind velocity and is accounted for in the value of the outside film coefficient of the composite wall or roof.
Heat gain through a wall is complicated by the fact that some of the heat passing through it is first stored and then released to the interior at a later time.
The color and nature of the external surface also affects the rate of heat transfer. A dark rough surface absorbs solar radiation raising the surface temperature whereas a light, smooth surface would reflect some of the radiation falling on it.
There are several methods for determining the heat gain through walls. The transfer function method uses a set of coefficients that relate an output function at a given time to the value of one or more driving functions at the current time and previous times. In the Total Equivalent Temperature Differential (TETD) method, various components of space heat gain are added together to get an instantaneous total rate of space heat gain which is then converted to an instantaneous space cooling load through the use of weight factors.
The Transfer Function method requires repeated cyclical computations to obtain steady state heat flow for the given hour. When coupled with hour-by-hour computations, this method requires large amounts of computer processing resources.
Heat gain = CLTDx Surface Areax U - Factor
The Loads Program uses the CLTD method to determine the heat gain through walls and roofs. CLTD values are based on specific wall and roof heat gains and are calculated for these structures using the transfer function method. CLTD values are derived from the transmission portion of the load, which can be expressed by
Qw=Uw Aw CLTD
The heat gain through walls (and roofs):
| Where: | Qw | = heat gain through wall, Btu/h |
| Uw | = overall heat transfer coefficient, Btu/h sq ft F | |
| Aw | = wall surface area, sq ft | |
| CLTD | = Cooling Load Temperature Difference for given hour, F |
The overall heat transfer coefficient for walls, Uw, is obtained from:

| Where: | Rw | = overall wall resistance, hr sq ft F/Btu |
| fi | = inside wall surface coefficient, Btu/h sq ft F | |
| fo | = outside wall surface coefficient, Btu/h sq ft F | |
| x1 ... xn | = thickness of each section of composite wall, in. | |
| K1 ... Kn | = conductivity of each section, Btu in./h sq ft F |

Heat Gain Through Doors
The heat gain through doors is due to conduction and infiltration. For the conduction portion, the load is calculated from:
Qdc = Ud A
| Where: | Qdc | = conduction heat gain through door, Btu/h |
| Ud | = heat transfer coefficient for door, Btu/h sq ftF | |
| Ad | = door area, sq ft | |
| To | = outdoor air temperature, F | |
| Ti | = indoor air temperature, F |
The heat transfer coefficient Ud is for the overall door including insulation and storm doors. When glass doors are exposed, they should be treated as windows.
For the infiltrated air portion of the load from doors, the infiltrated air quantity is based on the user-defined criteria of cfm/door area or door perimeter.
Heat Gain Through Windows
Windows are glass segments on wall exposures. Heat gain through windows is the transmission and solar heat gain through the glass surface adjusted for the effect of shadows cast on the glass by side fins, overhangs and recesses.
See Fig. 1-9 for the window geometry and shading features used in equations 18-23. The glass area in shade is calculated using these equations.
x = C tan γ γ = θ - ψ
| where: | x | = length of shadow cast by side fin, ft |
| C | = depth of side fin, ft | |
| γ | = wall solar azimuth angle, degrees | |
| θ | = solar azimuth angle, degrees | |
| ψ | = wall azimuth angle, degrees |
y = M tan β y = C sec γ tan β
| where: | y | = length of shadow cast by overhang, ft |
| M | = overhang depth in the sun azimuth plane, ft | |
| β | = sun altitude angle, degrees | |
| γ | = wall solar azimuth angle, degrees |
A1=W x( y - B )+ H x (x - D ) - ( y - B ) x (x - D )
A2=W x [H - A1]
| where: | A1 | = glass area in shade, sq ft |
| A2 | = glass area in sun, sq ft | |
| W | = glass width, ft | |
| H | = glass height, ft | |
| B | = distance of overhang from glass, ft | |
| D | = distance of side fin from glass, ft |
The solar heat gain factor (SHGF) is the total radiation on glass for the area A2 located in sunlight and the sum of diffuse and reflected radiation only for the glass area A1 located in the shade. Windows can be assigned a glass type from the Reference Library. The term glass type includes glass and shading device combinations. The Loads Program libraries contain properties of various glass types. Infiltration load through windows is a user-defined parameter as discussed in the section on doors. The section on infiltration details the calculation sequence for infiltrated air.

Heat Gain Through Skylights
Skylights are glass segments on horizontal or inclined exposures and are, therefore, assigned to roofs. Heat gain through skylights is the transmission and solar heat gain through the glass surface and the heat gain due to infiltration as discussed for doors and windows. The solar heat gain factor is the sum of the component of the sun's radiation intensity normal to the inclined surface and the diffuse radiation.
Is= IDN ( sinβx cosδ + cosβx cosγx sinδ )
| where: | Is | = solar radiation on given surface |
| IDN | = sun radiation intensity | |
| β | = sun altitude angle, degrees | |
| γ | = wall solar azimuth angle, degrees | |
| δ | = inclination of surface with horizontal degrees |
The solar radiation and transmission heat gain through the skylights is calculated from
Qrs = A SC SHGFmax CLF
Qrt= As Ug CLTD
| where: | Qrs | = solar radiation gain, Btu/h |
| Qrt | = transmission gain, Btu/h | |
| As | = skylight area, sq ft | |
| SC | = shading coefficient of glass | |
| Ug | = U-factor of glass, Btu/h sq ft F | |
| CLTD | = Cooling Load Temperature Difference, F | |
| SHGFmax | = Max. Solar Heat Gain Factor for orientation of surface, latitude, and month | |
| CLF | = Cooling Load Factor |
Heat Gain Through Floors, Partitions, and Ceilings
Heat gains through floors, partitions, and ceilings are assumed to occur through transmission only. The U-factor for the floor or partition and the temperature in the unconditioned space next to the floor or partition are used to determine the heat gains.
Qf = At Uf (Tu - Ti)
Qp = Ap Up (Tu - Ti)
| where: | Qf | = heat gain through floor, Btu/h |
| Qp | = heat gain through partition, Btu/h | |
| Af | = surface area of floor, sq ft | |
| Ap | = surface area of partition, sq ft | |
| Uf | = U-factor for floor, Btu/h sq ft F | |
| Up | = U-factor for partition, Btu/h sq ft F | |
| Tu | = conditioned space temperature, F | |
| Ti | = indoor temperature, F |
scripts f and p refer to floor and partition.
Infiltration
The infiltration cooling load through doors, windows, and skylights is the energy required to cool the outdoor air from the outdoor air enthalpy, (H1) down to the indoor air enthalpy, (H2).
Qinfiltration = 4.5 cfm (H1 - H2)
Qlatent = 4840 cfm (W1 W2)
Qsensible = 1.08 cfm (T1 T2)
| where: | cfm | = amount of infiltrated air, cu ft/min |
| H1 | = enthalpy of outdoor air at hour of calculation, Btu/lb | |
| H2 | = enthalpy of indoor air at room condition, Btu/lb | |
| 4.5, 4840, 1.08 | = constants for Standard Air |
The Loads Program recalculates these constants for air at conditions other than Standard.
Internal Loads
The Loads System analyzes cooling loads from several internal sources. They include
| ? | Heat gain from people |
| ? | Heat gain from lights |
| ? | Heat gain from equipment |
Equations 32 through 36 are concerned with internal load densities from these sources. For these equations, the Loads Program multiplies an ASHRAE equation by a factor, P, to account for hourly variations in the internal load densities.
Heat Gain From People
The total heat gain from people consists of sensible and latent gains. The total heat gain varies with the degree of activity of the occupants in the room. Fixed values for heat gain from people are used. These were previously adjusted to the normal percentage of men, women, and children for the different types of occupied spaces.
Qsensible = No. x sensible HG x CLF x P
Qlatent = No. x latent HG x P
| where: | Qsensible | = total sensible heat gain from people, Btu/h |
| Qlatent | = total latent heat gain from people, Btu/h | |
| No. | = maximum number of people in space | |
| HG | = total net gain/person for given type of space, Btu/h | |
| CLF | = cooling load factor for occupants | |
| P | = percent of maximum number of people at given hour |
Heat Gain From Lights
Some of the energy from lights is in the form of radiation which is first absorbed by the walls, floor and furniture, then released into the air. A percentage of a room's light energy can be assigned to the return air plenum (if one exists) to act as a plenum load. A Lights Profile expresses the hourly load from lights as a percentage of the maximum room load from lights.
The Cooling Load Factor method uses appropriate factors which take into account the type of light fixture used, type of air supply and return, space furnishings, space's thermal characteristics, the duration in which lights have been turned on. A set of factors expressing these parameters have been developed and are tabulated in the ASHRAE Handbook: 1981 Fundamentals as a-coefficient and b-classification, and are used in the selection of CLFs for lights.
The heat gain from lights is:
Qlights = INPUT x 3.413 x CLF x P1 x P2
| where: | Qlights | = heat gain from lights, Btu/h |
| INPUT | = total light wattage, watts | |
| CLF | = cooling load factor for lights | |
| P1 | = percent of maximum wattage in space at given hour | |
| P2 | = percent of light heat to room |
Heat Gain From Equipment
Variations from maximum design load in equipment heat gains are obtained by assigning a profile number to the equipment load. Heat gain from equipment can be sensible, latent or both, and can be entered in watts and Btu/h. The heat gain estimation is done by the Cooling Load Factor method. Appropriate CLF's for equipment were developed to reflect the timedelay effect of the radiant fraction of the sensible heat gain, in the same manner for other load components already discussed.
Heat gain from equipment:
Qeg (sensible)= sensible H.G. x CLF x P x 3.413 eg
Qeq (latent)= latent H.G. x P
| where: | Qeg | = heat loads from equipment, Btu/h |
| H.G. | = sensible or latent heat gain, Btu/h | |
| CLF | = equipment cooling load factor | |
| P | = percent of maximum equipment heat for the hour of calculation |
Heat Gain From Plenums
The Loads Program treats plenums as thermal areas which ultimately contribute to the total room heat load. The heat load components in a plenum heat balance are the load from lights, load from the space above the plenum, from the space below the plenum, from the exterior plenum walls, and heat to the return air stream. Some of these components may drop out for a given application, such as in the case of an interior plenum space or a plenum without heat contribution from lights.
Plenum Temperature Calculation
Fig. 1-10 shows the plenum configuration and different load elements. The block diagram presented in Fig. 1-11 depicts the logic for estimating the plenum temperature due to these loads. Distinction is made between the different types of return employed. Hence, the designer can specify a plenum space either with ducted return air, or let the return air flow directly in the plenum. In the case of ducted return, the Loads Program ignores the thermal gradient between the ducted air and plenum space, for the sake of simplicity.
From Fig. 1-10, the plenum heat balance is:
= Fc cfm (Tpl - TRM), Btu/h
Qair =Qwall + Qroof +Qlights +Qceiling
| where: | Qair | = heat into air flowing through plenum, Btu/h |
| Fc | = 1.08 for standard air | |
| Qwalls | = heat through plenum exterior walls, Btu/h |
=[(UA)wall + (CLTD)wall]
=[(UA)roof + (CLTD)roof], or [(UA)sa (Tpl-Tsa)]
| Qroof | = heat through plenum roof, or space above plenum, Btu/h |
| Qlights | = heat to plenum from lights, Btu/h |
| = watts x 3.413 x (% heat to plenum) x (percent of max. lights at hour of calculation) | |
| Qceiling | = heat through plenum ceiling, Btu/h |
=[(UA)ceiling (T pl - T RM)]
The Loads Program applies corrections for outside conditions only to the CLTD values. The inside conditions are analyzed based on the inside temperature of 78F on which the CLTD's were originally computed:
CLTDcorr=(CLTD+ LM)K +(78 - Tpl) +(To - 85)
| where: | LM | = correction for latitude and month |
| K | = correction for exterior color | |
| Tpl | = inside temperature, which is Tplenum in this case | |
| To | = (design outside dry-bulb - 1/2 of the daily range) |
Hence, the heat balance on the plenum is:
Fccfm (Tpl - TRM)= (UA)wall [(CLTD)olm + (78 - Tpl)]wall +
(UA)room [(CLTD)olm + (78 - Tpl)]roof +
Qlights - (UA)c (Tpl - TRM)
| where: | CLTDolm | = CLTD corrected for outside conditions and latitude/month only |
| Fc | = correction factor for air density and temperature |
rearranging and solving for plenum temperature;

The plenum heat balance above would also hold for the case where the space above the plenum is a floor not a roof. For this, the terms for the heat from the roof drop from the Tpl equation and are replaced by:
(UA) (Tpl - Tsa)
the Tpl equation for plenums under floors:

Cooling Load Through Plenums
Fig. 1-11 shows the iterative method for plenum temperature calculation. The load in cfm from each internal and external component is estimated in a modular form, except for the load from the room's ceiling. The load from the room's ceiling is calculated separately and then added to the sum of cfm's from other loads. The load from the ceiling is found from
Qceiling = Fc cfm (T plenum T RM)
Initially it is assumed that Tplenum is equal to room temperature, since it is the only known quantity by virtue of it being a design prerogative. Hence, for the first attempt, the load for the ceiling is actually zero. Next, the sum of all load cfm's is substituted into the plenum temperature equation and a value for Tpl is obtained. This Tpl is compared against the plenum temperature from the ceiling load module for convergence.
If the temperatures differ by more than 0.01F, an iterative procedure is initiated for the cfm from the ceiling module only. The sum of the cfm's from other load modules remain unchanged. The calculated Tpl from the preceeding step now replaces the Tplenum which was initially assumed to be at room (design) temperature, and the ceiling cfm is recalculated.
The new ceiling cfm is added to the cfm's from other modules and the new total cfm is plugged into the Tpl equation to obtain a new Tpl. This new Tpl is now compared to the Tplenum (which is not the design room temperature anymore, but had been equated to Tpl from previous step).
The iteration resumes till the two temperatures are within 0.01F, at which point the program goes into the loop one more time to calculate the ceiling load based on the stabilized plenum temperature.
Heating Loads
Transmission Losses
Transmission losses occur through the building envelope. The equations for determining the winter heating transmission losses include
Qg = Ug Ag (Ti - To)
Qd = Ud Ad (Ti - To)
Qw = Uw Aw (Ti - To)
Qt = Ut At (Ti - To)
Qs = Us As (Ti - To)
Qf = Uf Af (Ti - To)
Qp = Up Ap (Ti - To)
The subscripts g, d, w, r, s, f, and p refer to glass, door, wall, roof, skylight, floor, and partition.
| where: | Q | = heat loss by conduction, Btu/h |
| U | = overall heat transfer coefficient, Btu/h ft sq F | |
| A | = surface area, sq ft | |
| Ti | = design indoor temperature, F | |
| To | = outdoor temperature at selected design hour, F |
Infiltration
The infiltration heating load is the energy required to sensibly heat the outdoor air from the outdoor air temperature (To) up to the indoor air temperature (Tin).
Qsensible = Fc cfm (Tin - To)
| wehere: | cfm | = amount of infiltrated air, cu ft/min |
| To | = temperature of outdoor air at hour of calculation, F | |
| Tin | = temperature of indoors, F | |
| Fc | = constant for air condition = 1.08 for Standard Air |
The program recalculates this constant for air at conditions other than Standard.
Solar and Internal Gains
The Loads Program calculates the solar portion of heat gains through glass, but does not consider it in cfm estimation. All internal gains such as from occupants, lights and equipment are calculated by the Loads Program in heating load estimations and presented in output reports. However, these gains are not considered in cfm calculations.
Internal Losses
The Loads Program compensates for the heating load imposed by damper leakage of the cold primary air control boxes. This appears on the Room report as "primary air". The heat loss is found from:
Heat Loss= F1 x cfmcooling x Percent Primary Air [T room SSAT summer ]
| where: | Heat Loss | = heating load due to damper leakage, BtuH |
| Percent Primary Air | = input primary air percent, default = 10% | |
| Troom | = heating design room temperature, F | |
| SSAT | = temperature of the leaked cook air, F | |
| F1 | = air conversion factor |
System Types
The Loads Program analyzes two basic air system types:
| ? | Constant Volume Systems |
| ? | Variable Air Volume Systems |
Constant Volume
| ? | Constant Volume |
| ? | Constant Volume Reheat |
| ? | Multi-zone |
All of these systems share the same System Analysis method. Constant volume systems are based on the room peak loads and cfm. The zone and system cfm is the sum of the peak cfm for each room, although the rooms might peak at different hours. CV reheat systems may have a central reheat coil, a zone reheat coil, or both.
Variable Air Volume
Variable Air Volume systems include:
| ? | True VAV (cooling only) |
| ? | VAV Reheat |
Both systems share the same System Analysis method. For Variable Air Volume systems, the cfm for the rooms are based on the individual room peak loads. The Zone cfm is based on the room loads at the month and hour of the simultaneous peak of all the rooms in the zone. The System cfm is based on the zone loads at the month and hour of the simultaneous peak of all the zones in the system. VAV reheat systems may have primary reheat coils, zone reheat coils, or both
Required Supply Air Quantity and Quality
The thermal components of heat gain in a space are the Sensible Heat Gain (SHG) per hour and the Latent Heat Gain (LHG) per hour. The quantity and thermal quality of the air supplied to the space must, therefore, offset the sensible and latent heat gain per hour of that space in order to maintain the internal design conditions.
The supply air dry-bulb temperature is fixed based on practical considerations of cooling coil leaving temperatures. The mass of air supplied per hour to the space is, therefore, calculated to offset the peak SHG per hour of the space.
SHG = m x Cp x (tr - ts)
where: m= mass flow rate of air supplied to the space

| Cp | = specific heat at constant pressure = 0.240 Btu/Lb F |
| tr | = room design temperature for summer, F |
| ts | = supply air temperature for summer, F |
| SHG | = sensible heat gain in the space at peak hour and month, Btu/h |
Equation 53 is commonly expressed as

| where: | Qs | = summer supply air volume, cu ft/min |
| F1 | = conversion factor = 1.08 for standard air, Btu min/cu ft Hr F | |
| Δts | = summer room temperature differential, F = Troom - Tsupply |
Since the mass of air supplied to the space is fixed to offset the SHG, the moisture content of the mass of air supplied per hour must be such that it offsets the LHG per hour of the space.
LHG=m x (Wr -Ws) x hfg
| where: | LHG | = latent heat gain in the space, Btu/h |
| m | = mass flow rate of air supplied to the space, Lb/hr | |
| Wr | = room humidity ration, Lb water/Lb dry air | |
| Ws | = supply air humidity ration, Lb water/Lb dry air | |
| hfg | = (specific enthalpy of saturated water vapor - specific enthalpy of saturated liquid water), Btu/Lb |
The required moisture content of the air to be supplied to the space is obtained by rearranging equation 55.

The factor F2 converts volume flow per minute to mass flow per hour.
Equations 54 and 56 are used by the Loads Program to determine the quantity and quality of air that must be supplied to the space to maintain the required space conditions.
Winter
The total heat loss from the space is considered in determining the required supply air quantity and quality in winter. The winter supply air quantity for an all air system is obtained from

| where: | THL | = total heat loss from the space, Btu/h |
| = losses due to transmission and infiltration | ||
| Qw | = winter heating supply air quantity, cu ft/min | |
| Δtw | = winter room temperature differential | |
| = Tsupplywinter - Troomwinter | ||
| F1 | = conversion factor, Btu min/cu ft Hr F |
The moisture content of the supply air would be determined by the required winter humidification load as expressed in the System Analysis portion.
Room Analysis
Minimum Room Air Quantities
Minimum room air quantities are defined using the room ventilation criteria fields in a reference library table or data forms. Minimum ventilation criteria data is optional.
Minimum supply, outdoor, and return air quantities can be specified on the basis of cfm/sq ft, cfm/person, or air changes/hour. Outdoor and return air quantities can also be specified as percent of the supply air quantity. In addition, return air can be expressed as a room pressure ratio of supply air to return air.
The cfm used in System Analysis is the cfm due to room loads. The minimum cfm, if greater than Load cfm, is used to calculate the amount of summer reheat that would be necessary to keep the room at the specified internal design temperature.
The cooling reheat load is calculated for each room with minimum cfm that exceeds load cfm. The individual room reheats are added together to arrive at the required reheat at the zone.
RRHL= F1 x (cfmmin - cfmload) (RT - RSAT )
ZRHL= RRHL1 + RRHL2 + ... + RRHLn
| where: | RRHL | = room reheat load, Btu/h |
| ZRHL | = zone reheat load, Btu/h | |
| cfmmin | = Room Minimum Air cfm for summer | |
| cfmload | = Room Load cfm for summer | |
| RSAT | = summer room supply air temperature, F | |
| RT | = summer room design temperature, F |
The reheat loads here are "resultant reheat" due to a minimum air cfm which exceeds the load cfm, and are not to be confused with the reheat loads for reheat systems. Reheat loads RRHL and ZRHL are calculated and reported, but are not acted upon or considered for System Analysis. This enables the designer to make a choice between changing the design conditions to avoid reheat or accepting the resultant energy penalty.
For Variable Air Volume systems, minimum air entries are ignored since VAV systems, by definition, have no "minimum" air to maintain regardless of load variations.
Air Quantities Based on Heat Gain and Losses
Winter heat losses are based on a single winter design month and hour. Summer heat gains must, however, be calculated for all hours of a typical day for each summer month in order to determine air quantities that might occur at different peak times.
Fig. 1-12 shows a profile the Loads Program generates for room heat gains during summer months.
Fig. 1-13 shows a profile of zone heat gains with room components.
Fig. 1-14 shows a profile of plant and systems hourly and peak loads.
The Loads Program uses these profiles to determine the months and hours when the room, zone, system, and plant are at their peak load conditions.
The Loads Program analyzes the cooling coil load on each system at each hour and month of plant operation to determine the system peak hour and month. The analysis includes all load sources on the cooling coil such as supply/return fans and ductwork, room loads, return air from plenums, mix air and ventilation loads, and any input system and zone reheat values. These hourly loads are added together at each hour to determine the plant profile. For example, the plant load for hour 15 is the total of the loads on each system at hour 15. The plant peak hour is the hour where the total loads for the system are greatest.
Fig. 1-14 illustrates the hourly loads characteristics for a plant incorporating three air handling systems with each system peaking at a different hour.
Summer Air Quantity
The room supply air quantity is calculated on the basis of sensible heat gain using the design supply air temperature.

where the subscript s denotes summer.
| Qs | = supply air quantity to the space, cu ft/min |
| SHG | = Sensible Heat Gain, Btu/h |
| RTs | = design indoor temperature for the room, F |
| RSATs | = design supply air temperature, F |
| F1 | = conversion factor, Btu min/cu ft Hr F |
Winter Air Quantity
For an all air heating system, the required supply air quantity is calculated from:

where the subscript w denotes winter.
| and: | Qw | = room supply air quantity, cu ft/min |
| THL | = total heat losses from the room, Btu/h | |
| = losses due to transmission and infiltration | ||
| RSATw | = design supply air temperature, F | |
| RTw | = design indoor temperature, F | |
| F1 | = conversion factor, Btu min/cu ft Hr F |
Interior Rooms
Interior Rooms are examined for cooling/heating load requirements. For heating systems, interior rooms which require winter cooling because of presence of a cooling load would result in zero cfm heating for these rooms. This will be apparent from the direction of heat gains to the space and the magnitude of the SSATw.
Zone Analysis
The Loads Program room analysis assumes that the internal design condition is the most critical room criteria. Zone supply air temperatures are fixed for winter and summer to accommodate the internal design conditions for each room. For reheat systems, the zone supply air temperature would reflect the input design F reheat at the individual zones. This leads to zones within the same AHU that have different supply air temperatures, according to whether they have zone reheat. The designer, hence, has the flexibility of specifying reheat at some zones, while other zones within the AHU can be left without zone reheat. See the "Reheat Loads" section, below.
Air Quantities
The zone supply air quantity for a constant volume system is the sum of the peak maximum air quantities of all the rooms in the zone. Room air quantities are calculated at the different months and hours when each of the rooms reach their maximum SHG.
Qz = qz 1t 1 + qz 2t 2 + ... + qzntn
| where: | Qz | = zone air quantity of the Constant Volume System, cu ft/min |
| qzi | = peak supply air quantity for room i in the zone, (i = 1 to n), cu ft/min | |
| ti | = time (month and hour) of maximum SHG for room i, (i = 1 to n) | |
| n | = number of rooms in the zone |
The zone supply air quantity for a variable air volume system is the sum of the air quantities of all the rooms in the zone calculated at the month and hour when the simultaneous peak SHG of all the rooms in the zone occurs.
Qz = qz 1tz + qz2tz + ... + qzntz
| where: | Qz | = zone air quantity of the Constant Volume System, cu ft/min |
| qzi | = supply air quantity for room i in the zone, (i = 1 to n) at time tz, cu ft/min | |
| tz | = time (month and hour) of maximum SHG for the zone | |
| n | = number of rooms in the zone |
The zone diversity of a VAV System is the ratio of the Variable Air Volume zone air quantity to the Constant Volume zone air quantity.

Air Temperature
The summer and winter zone supply air temperatures are determined from user input. The required room design temperatures of all rooms in the zone will be maintained at all times. The air quantities for those rooms are calculated at the peak conditions.
The summer system supply air temperature is determined by the data entered on the proj_AHU form. For reheat systems, at the AHU (central), the SSAT would reflect the input F rise for System Reheat. Reheat F rise may be entered at the reheat coils, at the zone, or both. The winter system supply air temperature is entered on the proj_AHU form.
Reheat Loads
System Reheat
Two fields on the proj_AHU form are involved in determining reheat loads. They are the F System Reheat field and the summer design supply temperature field. The latter field also represents the SSAT or System Supply Air Temperature. The Loads Program looks upon the SSAT as the temperature leaving the primary reheat coil. If you enter a quantity in the F system reheat field, the SSAT does not change. However, the cooling coil leaving temperature will decrease. You can change the SSAT only if you enter a temperature in the summer design supply temperature field.
Fig. 1-15 shows a Blow-thru AHU with a cooling coil and a reheat coil. Assuming that you enter a SSAT of 59F and system reheat of 7F, the temperature of the air leaving the cooling coil is then 52F. Changing the system reheat to 0F means the air leaving the cooling coil is now at the 59F SSAT you previously entered, and the unit does not have reheat.
Zone Reheat
Using Fig. 1-15, the air reaching the individual zones of the system is at the SSAT of 59F, regardless of what you enter in the F system reheat field. Of the three zones shown in the figure, one has a 5F reheat input, the second has a 3F reheat input and the third has no reheat. The results in zone rooms supplied with air at 64F, 62F, and 59F for each respective zone. Hence, the Loads Program increments the input SSAT on the proj_AHU form by the amount of F zone reheat entered on the zone form to arrive at individual zone supply air temperature.
Psychrometric Analysis
For each air handling system, the air is analyzed psychrometrically and the properties of air at each point are reported on the System report. For central reheat systems with no zone reheats, the reported point conditions are at the discharge of the reheat coil. For zone reheat systems with no central reheat, the point that is reported is the one where you have entered the highest zone reheat. Namely, for a system with SSAT = 58F and zone reheats of 3F and 5F, the reheat point reported on the System report is at 58 + 5 = 63F.
The above is also true for reheat systems with both central and zone reheat. Again, the reported reheat point is at the highest zone reheat. For the same example, an entry of 6F would still keep SSAT at 58F and the reheat point at 63F.
Designers should note that they need to establish individual room condition lines for each zone. The lines emanate from the respective zone reheat point to the average space temperature for each zone. In the above example, the reheat points were 61F and 63F. Alternatively, draw a room condition line for each room zone.
The psychrometric analysis a designer sees on the Systems report implies a room condition line (between the reheat point and the space point) only when the reheat is exclusively at the system. For the other two reheat cases (system and zone, or zone only), there are no individual room condition lines implied. The reported point is that of the highest zone reheat. In all cases, the BtuH reheat reported covers all reheat input whether it is at the zone, system, or both.
Qreheat total = F1 x System cfm xoF System Reheat +
F1 x (Zone cfm xoF Zone Reheat)zone i
| where: | Qreheat total | = BtuH total reheat quantity reported on System Report |
| i | = 1 to n, n is the number of zones that have reheat |
System Air Quantities
Constant Volume Supply
The supply air quantity of a constant volume system is the sum of the peak maximum air quantities of all the rooms in the system. The room air quantities are calculated at different months and hours when each room reaches its peak SHG.
Qr = qr1t1 + qr2t2 + ... +qrntn
| where: | Qr | = room air quantity of the Constant Volume System, cu ft/min |
| qri | = peak supply air quantity for room i in the system (i = 1 to n), cu ft/min | |
| ti | = time (month and hour) of maximum SGH for room i (i = 1 to n) | |
| n | = number of rooms in the zone |
Variable Air Volume Supply
The supply air quantity of a variable air volume system is the sum of the air quantities of all the rooms in the system at the month and hour when the simultaneous peak SHG of the system occurs.
Qr = qr1t1 + qr2t2 + ... +qrntn
| where: | Qr | = room air quantity of the VAV system, cu ft/min |
| qri | = peak supply air quantity for room i in the system (i = 1 to n), at time tr, cu ft/min | |
| ti | = time (month and hour) of maximum SGH for the room | |
| n | = number of rooms in the zone |
System Diversity
The system diversity of a VAV System is the ratio of the VAV system air quantity to the Constant Volume system air quantity.

Return Air
The return air quantity of each room can be specified on the basis of percent of room supply air, air changes per hour, cfm/sq ft, or supply air to return air pressure ration. The return air quantity of the system is the sum of the return air quantities of all the rooms in the system.
QR = qr1 + qr2 + .. +qrn
| where: | QR | = return air quantity, cu ft/min |
| qri | = return air quantity from room i (i = 1 to n), cu ft/min | |
| n | = number of rooms |
Exhaust Air
The exhaust air quantity of each room can be specified on the basis of percent of room supply air, air changes per hour, cfm/sq ft, or supply air to exhaust air pressure ratio. The total exhaust air quantity from the system is the sum of the exhaust air quantities of all the rooms in the system.
QE = qe1 + qe2 + .. +qen
| where: | QE | = exhaust air quantity, cu ft/min |
| qei | = exhaust air quantity from room i (i = 1 to n), cu ft/min | |
| n | = number of rooms |
Outdoor Air
The outdoor air quantity of each room can be specified on the basis of percent of room supply air, air changes per hour, cfm/sq ft, or cfm/person. Room outdoor air quantities are expressed as percent outdoor air in order to calculate the maximum percent outdoor air of the system.
The outdoor air quantity of the system can be specified on the basis of percent of total supply air, the average value of the percent outdoor air of all the rooms in the system or the maximum value of the percent outdoor air of all the rooms.
Option-1:

Option-2:

Option-3:

| where: | Qo | = outdoor air quantity, cu ft/min |
| P | = percent of total supply air | |
| qoi | = outdoor air quantity of room i (i = 1 to n), cu ft/min | |
| qsi | = supply air quantity of room i (i = 1 to n), cu ft/min | |
| Pomax | = maximum value of percent outdoor air for rooms 1 to n | |
| n | = number of rooms |
The system outdoor air quantity will be set as the difference between the system supply air quantity, Qs, and the return air quantity, Qr, if this is greater than the outdoor air quantity calculated from equations 70, 71, and 72. This situation might occur if the exhaust air quantity Qe from the system is high.
Qo = Qs - Qr
Spill Air
The spill air quantity is the excess return air when the return air quantity, Qr, is greater than the outdoor air quantity, Qo.
Qsp = Qr - Qo
System Air Conditions
Fig. 1-16 shows the psychrometric process of the air from the leaving side of the cooling coil and back to the entering side of the coil.

All the rooms in the system are treated as one space in the system analysis.
Space Condition
The space dry-bulb temperature is the weighted average of the dry-bulb temperatures of all the rooms in the system. Room relative humidities are converted to humidity ratios and the weighted average humidity ratio value of all the rooms represents the humidity ratio of the space.

| where: | Ts | = space dry-bulb temperature, F |
| ti | = design dry-bulb temperature for room i (i = 1 to n), F | |
| Ws | = space humidity ratio, Lb/Lb | |
| wi | = design humidity ratio for room i (i = 1 to n), Lb/Lb | |
| Qi | = room supply cfm for room i (i = 1 to n), cu ft/min |
Return Air
The return air dry-bulb and humidity ratio leaving the space are the weighted average values.

Wr = Ws
Qr = q1 + q2 + ... + qn
| where: | Tr | = return air dry-bulb temperature, F |
| Wr | = return air humidity ratio, Lb/Lb | |
| Qr | = total return air quantity, cu ft/min | |
| ti | = dry-bulb temperature for ducted return or plenum temperature if plenum return, for room i (i = 1 to n), F | |
| qi | = return air quantity for room i (i = 1 to n), cu ft/min | |
| Ws | = space humidity ratio, Lb/Lb |
Equation 77 gives the combined return air temperature. The load from light heat to the plenums is partially used to increase the temperature of the return air. The remainder of the light heat constitutes a recontributed load on the space where it had originated, across the suspended ceiling. Other plenum loads (such as from the roof, exterior walls, etc.) act in the same double-duty of raising the return air temperate as well as imposing a cooling load on the room.
The amount of heat to the combined return air, due to all plenum load sources, is:
Qret.air= F1 x cfmzone x (Tr - Ts)
| where: | Qret.air | = amount of heat to return air, BtuH |
| cfmzone | = sum of zone cfm: at Room Peak Hours for CV Systems at Zone Peak Hours for VAV Systems | |
| Ts | = from equation 75 | |
| Tr |

|
Return Duct and Return Fan
Temperature rise across the return ductwork and/or the return fan may come from direct userinput or through translation of the BtuH amount of heat into a F temperature rise:
Hence the dry-bulb temperature after the return duct loss or at the fan discharge may be found. The moisture content of the air stays essentially the same as when returned from the space.
Tret. = Tr + oF Return Fan Rise + 1oF Return Duct Rise
Ws = Wplenum = WR. fan = Wret.
| where: | Tret. | = return air temperature, F |
| Tr | = from equation 77 | |
| Ws | = moisture content of the space, Lb/Lb, from equation 76 |
Knowing the dry-bulb temperature and the moisture level, the enthalpy of the return air is found from:
Hret. = 0.24t+(1060 x 0.444t) Wret.
| where: | Hret. | = enthalpy at duct loss point or at return fan discharge |
| Wret. | = return air moisture level, Lb/Lb, same as Ws from equation 76 |
Outdoor Air
The outdoor air dry-bulb temperature, To, and humidity ration, Wo, are the outdoor conditions at the month and hour when the system is at its peak hour and month.
Mixed Air
The mix air condition is the weighted average value of the return air including any plenum return fan return duct heat gains and outdoor air conditions.

| where: | Tmix | = mix air dry-bulb temperature, F |
| To | = outdoor air temperature, F | |
| Qs | = supply air quantity, cu ft/min | |
| Qo | = outdoor air quantity, cu ft/min | |
| Tret. | = return air temperature, F | |
| = the greater of return fan temperature, return duct temperature, return plenum/ducted temperature, or room temperature | ||
| Wmix | = mix air humidity ratio, Lb/Lb | |
| Wo | = outdoor air humidity ratio, Lb/Lb | |
| Wret. | = return air humidity ratio, same as Ws, Lb/Lb | |
| hmix | = enthalpy of mix air, Btu/Lb | |
| ho | = enthalpy of outdoor air, Btu/Lb | |
| hret | = enthalpy of air at return air point (return fan, plenum/ducted, return duct, or room |
The segment of the coil load that offsets the mix air may be found from:
Qmixtotal = Qmixsensible + Qmixlatent
Qmixsensible = F1 cfm (Tmix - Tret.)
Qmixlatent = F2 cfm (Wmix -Wret.)
Cooling Coil Analysis
The cooling load at the primary cooling coil accounts for the space SHG and LHG, ventilation SHG and LHG, and sensible heat gains to return air, ductwork, and fans.
Coil Entering Air Condition
The coil entering air condition is the mix air condition, for a draw-thru coil-fan arrangement.
Tec = Tmix
hec=hmix
Wec=Wmix
The fan heat gain is added to the mix air condition to obtain the coil entering dry-bulb temperature for a blow-thru unit.

Tec = Tmix + oF Supply Fan User - Input
hec= hs.fan = 0.24 Ts.fan + (1060 x 0.444 Ts.fan) Wec
Wec = Wmix
| where: | Tec | = coil entering air dry-bulb temperature, F |
| Wec | = coil entering air humidity ratio, Lb/Lb | |
| SFHG | = supply fan heat gain, Btu/h | |
| Qs | = supply air quantity, cu ft/min | |
| F1 | = conversion factor, Btu min/cu ft Hr F | |
| Ts.fan | = temperature of air at supply fan discharge, F | |
| hec | = enthalpy of coil entering air, Btu/Lb |
Cooling Coil Leaving Air Condition
The required cooling supply air dry-bulb temperature is entered in the program. The supply temperature is decreased to account for the temperature rise through the ductwork. For a draw-thru unit, the temperature is further decreased to account for the fan heat gain. The SSAT is further decreased by any input F reheat at the system (AHU) level.
TLC = SSAT - Td - System Reheat Blow - Thru
or
TLC= SSAT - Td -Ts.fan - System Reheat Draw - Thru
| where: | Tk | = required coil leaving air dry-bulb temperature, F |
| Td | = temperature rise through supply ductwork, F | |
| SSAT | = user-input system supply air temperature, F | |
| SFHG | = supply fan heat gain, Btu/h | |
| Ts.fan | = user-input supply fan temperature rise, F |
The required cooling supply air humidity ratio is calculated to offset the total latent heat gain in the system space.

similarly for enthalpy of leaving air:

| where: | Wic | = required coil leaving air humidity ratio, Lb/Lb |
| Wec | = humidity ratio of the air entering the coil, Lb/Lb | |
| CLL | = total latent load on the coil, Btu/h | |
| Qs | = supply air quantity, cu ft/min (Fan cfm) | |
| CTL | = total load on coil, BtuH |
F2 and F3 are conversion constants based on air quantities.
Cooling Load Across Coil
Fig. 1-16 shows the psychrometrics for draw-thru and blow-thru fan arrangements. The load across the cooling coil is determined by the air conditions at the entering and leaving sides of the coil. This load comprises all sensible and latent loads of the system.
The Loads Program breaks the load across the coil into individual load segments. These represent the loads from the supply fan, supply duct, space plenums, return duct, return fan and mix air. The air condition at each point is reported on output reports. This is useful to the designer, who now can produce a psychrometric presentation of the system.
Knowing that latent loads are introduced only at the space and the mix point, the total load on the coil may be obtained through the summation of the individual load segments:
CTL = SFH + SDH + REHEAT + ROOMS + RETURN + RDH + RFH + MIX
| where: | CTL | = total load on coil, BtuH |
| SFH | = heat from supply fan, sensible, BtuH = F1 x cfm x Supply Fan F Rise | |
| SDH | = heat from supply duct, sensible, BtuH = F1 x cfm x Supply Duct F Rise | |
| REHEAT | = reheat loads entered at system and zone levels = F1 x F Input x cfm, BtuH | |
| ROOMS | = room loads, total, BtuH | |
| RETURN | = return air load, sensible, BtuH = F1 x cfm x (tr - ts); see equations 75 and 77 | |
| RDH | = heat from return duct, sensible, BtuH = F1 x cfm x Return Duct F Rise | |
| RFH | = heat from return fan, sensible, BtuH = F= F1 x cfm x Return Fan F Rise x cfm x Return Fan F Rise | |
| MIX | = heat to mix air, total, BtuH; see equations 89, 90, and 91 |
Knowing that the latent loads on the coil are introduced at the rooms and at the mix point, the Coil Latent Load (CLL) can be expressed as:
CLL = ROOMS latent load + MIX latent load
where the first term is obtained from the summation of room latent loads at the system level and the second term is obtained from equation 90. Note that the CTL and the CLL (equations 103 and 104) were used to arrive at the leaving air enthalpy and humidity ratio (equations 101 and 102, respectively). The sensible load on the coil (CSL) may be expressed as:
CSL = CTL - CLL
The sensible heat ratio for the coil may be expressed as:

Ventilation Loads
The sensible component of the ventilation load may be expressed as:
VSL = F1 x Qo x (To.a. - Ts)
The latent component of the ventilation load may be expressed as:
VLL = Fs x Qo x (Wo.a. Ws)
The total ventilation load is expressed as:
VTL = VSL + VLL
| where: | Qo | = outdoor air quantity for ventilation, cu ft/min |
| To.a. | = outdoor air temperature at peak hour and month, F | |
| Ts | = space temperature, F | |
| F1 | = air conversion factor = 1.08 for standard air | |
| F2 | = air conversion factor = 4840 for standard air | |
| VTL | = total ventilation load, BtuH | |
| VSL | = sensible ventilation load, BtuH | |
| VLL | = latent ventilation load, BtuH | |
| Ws | = humidity ratio of space, Lb/Lb | |
| Wo.a. | = humidity ratio of outdoor air at peak hour and month (summer), Lb/Lb or at O.A. design DB/WB (winter), Lb/Lb |
The psychrometric analysis for the system is always at the system peak hour and month, which is not necessarily the hour of maximum outdoor air temperature. The Ventilation Total Load (VTL) for the system is at the system peak hour. Similarly, the plant ventilation load is at the plant peak hour.
System Checks and Warnings
Check for Saturation Curve Cross-Over
The input SSAT is decremented by any supply duct and/or supply fan temperature rises specified by the designer. The resultant lower temperature is the temperature of the air leaving the cooling coil (TLC) from equation 99 or 100. TLC may lie anywhere along its constant temperature line. The Loads Program fixes the location of TLC at its moisture level leaving the coil (WLC). TLC may be on the saturation curve or at the right hand side of the saturation curve but cannot possibly cross-over.
With this in mind, an exaggerated input value for the rise across the duct and/or fan may push TLC to the left hand side of the saturation curve. Similarly, a SSAT that is too close to the saturation curve might not have enough sensible temperature range (between the SSAT and the saturation curve) to accommodate the input duct/fan temperature rises. This would also put TLC on the left side of the saturation curve.
The Loads Program checks for such irregularities and issues a warning message to alert the designer when the input conditions cannot be met psychrometrically. The check is done by stipulating that the coil leaving air dry-bulb, TLC must be greater than or equal to the dewpoint temperature at the input SSAT and the moisture content of the air leaving the coil (WLC). Namely,
TLC ≥ (Tdewpoint )SSAT,W LC
The expression:
[SSAT - (Tdewpoint )SSAT,W LC] ≥ [Temperature rise duct and / or fan ]
indicates to the designer the fact that the input rise across the duct and/or fan must not exceed the difference between the input SSAT and its dewpoint temperature at the coil's leaving moisture content.
Check for Coil Freeze-up
The Apparatus Dew Point Temperature (ADP is obtained at the intersection of the Coil Condition Line with the Saturation Curve. A Coil Condition Line that is too steep may result in an unfavorable intersection with the saturation curve (or no intersection at all) at which the ADP constitutes a coil freeze hazard. Bearing in mind that there is no substitute for a psychrometric chart analysis in an air conditioning system design, the Loads Program provides a check guideline to warn the designer against low ADPs that may lead to coil freeze-ups.
The check sub-routine is meant to be used as a quick check, not a mathematically exact solution. It compares the Coil Sensible Heat Ration, CSHR from equation 106, against a built-in CSHR of 0.610 that would result in an ADP of approximately 38F. A warning message notifies the designer in such cases. Designers are urged to draw the system on a psychrometric chart and examine the ADP temperature.
System Heating Load for Winter
The system heating load consists of these individual loads:
Heating Coil Load, (HCL)
Heating Ventilation Load, (HVL)
Heating Humidification Load, (HHL)
Minimum Air Load, (ZEH)
The Heating Coil Load and Heating Ventilation Load are essentially sensible in nature.
The Total System Heating Load (TSHL) is the sum of the Heating Coil Load and Heating Humidification Load:
TSHL = HCL + HVL + HHL
The Minimum Air Loads are calculated and reported but not acted upon or considered in coil capacity.
Heating Coil Load
The heating coil load (HCL) is the sum of all the total heat losses at the rooms. The coil's cfm is the sum of the individual room cfm's calculated from the room's total heat losses.
cfm = ∑ Room cfm
HCL= ∑ Room THL
Both HCL and the heating cfm are based on the input winter supply air temperature. All credits for heat gains from fans and heat losses are ignored.
Heating Ventilation Load
The load imposed by outdoor ventilation air is expressed as:
HVL = Qo x F1 x (Ts - To.a.)
| where: | HVL | = heating ventilation load, sensible, Btu/h |
| Qo | = outdoor air quantity, cu ft/min | |
| F1 | = conversion factor = 1.08 for air at standard conditions, Btu min/cu ft Hr F | |
| Ts | = space temperature for the heating season (equation 75), F | |
| To.a. | = design outdoor air temperature, heating season, F |
Heating Humidification Load
The winter humidification load is made up of two components:
Ventilation outdoor air load, latent; (HLo)
Infiltration outdoor air load, latent; (HLi)
Humidification required for ventilation outdoor air is calculated by
HLo = Qo x F2 x (Ws -Wo.a.)
| where: | Wo.a. | = humidity ratio of outdoor air at minimum outdoor air temperature, winter, Lb/Lb |
| HLo | = air system humidification load in winter, Btu/h | |
| Qo | = ventilation outdoor air quantity, cu ft/min | |
| Ws | = space humidity ratio, heating season, Lb/Lb |
The factor F2 converts volume flow per minute to mass flow per hour.
The make-up humidification for infiltration is obtained from:
RHLi = IQi x F2 x (Wi -Wo)
HLi = RHL1 + RHL2 + .. + RHLn
| where: | THLi | = humidification due to infiltration for room i, Btu/h |
| IQi | = infiltration air quantity in room i, cfm | |
| Wi | = humidity ratio of room i, Lb/Lb | |
| Wo | = humidity ratio of outdoor air in winter, Lb/Lb | |
| HLi | = total humidification load due to infiltration, Btu/h | |
| n | = number of rooms in system. |
The winter humidification load is added to the other winter heating loads to size the plant. If the system goes to the economizer cycle during the intermediate seasons, then the humidification load during these periods may be greater than the winter load. The Loads Program calculates and reports the humidification load during the intermediate season using 100 percent outdoor air. This information can be used to size the humidifier if it is greater than the winter load.
HLi = Qeco x F2 x (Ws - Weco)
| where: | HLeco | = humidification load during intermediate season, Btu/h |
| Qeco | = supply air during economizer cycle (100% outdoor air), cu ft/min | |
| Weco | = humidity ratio of outdoor air in the intermediate season taken at 50F and 50% relative humidity, Lb/Lb | |
| Ws | = humidity ratio of system space, Lb/Lb |
The factor F2 converts volume flow per minute to mass flow per hour.
The Heating Humidification Load is the sum of HLo and HLi
HHL = HLo + HLi
The Total System Heating Load is as expressed in equation 112.
TSHL = HCL + HVL + HHL
Minimum Air Loads
For CV systems with minimum air cfm greater than the load cfm, the Loads Program calculates the amount of excess heating that would result and report it as a warning message. The excess heating would lead to a rise in room temperature, if the minimum cfm is considered and can be calculated by:

| where: | REH | = excess room heating load, BtuH |
| ZEH | = excess zone heating load, BtuH | |
| RT | = room design temperature, F | |
| Tsupply | = input system supply air temperature (winter), F |
The excess heating is recorded but not considered. No deductions of the heating coil capacity result due to the reported excess heating.






